题目内容
在直角坐标系中，A（-3，2），
=（3+5cosθ，-2+3sinθ）（θ∈R），则B点的轨迹方程是 ．
| AB |
考点：椭圆的参数方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：设B（x，y），利用A（-3，2），
=（3+5cosθ，-2+3sinθ），可得x=5cosθ，y=3sinθ，消去参数，可得B点的轨迹方程．
| AB |
解答：
解：设B（x，y），则
∵A（-3，2），
=（3+5cosθ，-2+3sinθ），
∴x=5cosθ，y=3sinθ，
∴
+
=1．
故答案为：
+
=1．
∵A（-3，2），
| AB |
∴x=5cosθ，y=3sinθ，
∴
| x2 |
| 25 |
| y2 |
| 9 |
故答案为：
| x2 |
| 25 |
| y2 |
| 9 |
点评：本题考查椭圆的参数方程，考查向量知识的运用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知命题p：“x＞3”是“x2＞9”的充要条件，命题q：“?x0∈R，x0-2＞0”的否定是“?x0∈R，x0-2＜0”（ ）
| A、“p∨q”为真 |
| B、“p∧q”为真 |
| C、p真q假 |
| D、p，q均为假 |
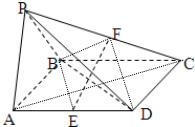已知四棱锥P-ABCD是底面为平行四边形，面PAB⊥面ABCD，△PAB为正三角形，且AB=已知cos（60°+α）=
，且α为第三象限角，则cos（30°-α）+sin（30°-α）的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|