题目内容
如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，P是侧棱CC1上的一点，CP=m，试确定m，使得直线AP与平面BDD1B1所成角的正切值为3
| ||
| 19 |
考点：直线与平面所成的角
专题：空间角
分析：直接根据已知条件求出线面的夹角，进一步解直角三角形求得结果．
解答：
解：在棱长为1的正方体ABCD-A1B1C1D1中，P是侧棱CC1上的一点，直线AP与平面BDD1B1所成角，
即∠APC，
所以解得：AC=
tan∠APC=
=
=
解得：m=
解：在棱长为1的正方体ABCD-A1B1C1D1中，P是侧棱CC1上的一点，直线AP与平面BDD1B1所成角，即∠APC，
所以解得：AC=
| 2 |
tan∠APC=
| AC |
| PC |
| ||
| m |
6
| ||
| 19 |
解得：m=
19
| ||
| 42 |
点评：本题考查的知识要点：线面的夹角及解直角三角形知识，属于基础题型．
练习册系列答案
相关题目
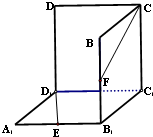将边长为l的三个正方形面板粘合成一个空间图形，其水平放置的直观图如图所示．
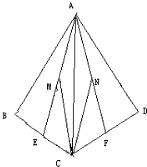如图，在四面体ABCD中，M、N分别是△ABC和△ACD的重心，求证：