题目内容
已知直线l过定点A(1,2),与x轴交点在(-3,0)和(3,0)两点之间,求直线l在y轴上的截距的取值范围.
考点:恒过定点的直线
专题:直线与圆
分析:设直线l的斜率为k,则直线l的方程为:y-2=k(x-1),结合直线l与x轴交点在(-3,0)和(3,0)两点之间,可得k的范围,令x=0,可得y的取值范围.
解答:
解:∵直线l过定点A(1,2),
设直线l的斜率为k,
则直线l的方程为:y-2=k(x-1),
令y=0,则x=1-
,
由直线l与x轴交点在(-3,0)和(3,0)两点之间,
∴-3<1-
<3,
解得:k<-1,或k>
,
令x=0,则y=2-k,
则y<
,或y>3,
即直线l在y轴上的截距的取值范围为(-∞,
)∪(3,+∞)
设直线l的斜率为k,
则直线l的方程为:y-2=k(x-1),
令y=0,则x=1-
| 2 |
| k |
由直线l与x轴交点在(-3,0)和(3,0)两点之间,
∴-3<1-
| 2 |
| k |
解得:k<-1,或k>
| 1 |
| 2 |
令x=0,则y=2-k,
则y<
| 3 |
| 2 |
即直线l在y轴上的截距的取值范围为(-∞,
| 3 |
| 2 |
点评:本题考查的知识点是直线的点斜式方程,直线的截距,难度不大,属于基础题.

练习册系列答案
相关题目
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
=a,
=b,则
等于( )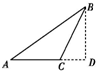
| AB |
| AC |
| BD |

A、
| ||
B、
| ||
C、
| ||
D、
|
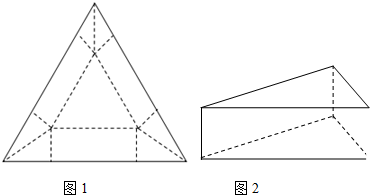
 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为
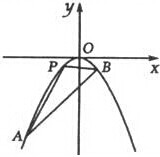 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,