题目内容
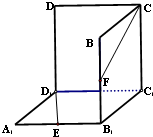 将边长为l的三个正方形面板粘合成一个空间图形,其水平放置的直观图如图所示.
将边长为l的三个正方形面板粘合成一个空间图形,其水平放置的直观图如图所示.(1)若E、F分别是A1B1、BB1的中点,试判断D1E与CF是否共面,并说明理由;
(2)以此空间图形为盛水容器,如果能保证粘合处都不漏水,那么此容器最多能盛多少体积的水?
考点:棱柱、棱锥、棱台的体积,由三视图求面积、体积
专题:空间位置关系与距离
分析:(1)连结EF,CD1,A1B,由已知得A1D1CB是平行四边形,由此能证明D1E与CF共面.
(2)最多能盛水的容积等于三棱锥C1-B1D1C的体积.
(2)最多能盛水的容积等于三棱锥C1-B1D1C的体积.
解答:
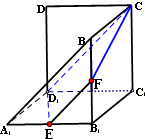 解:(1)如图,连结EF,CD1,A1B,
解:(1)如图,连结EF,CD1,A1B,
∵E、F分别是A1B1、BB1的中点,∴EF∥A1B,…(2分)
∵A1D1
B1C1,B1C1
BC,∴A1D1
BC,…(3分)
∴A1D1CB是平行四边形,∴A1B∥CD1,…(4分)
∴EF∥CD1,…(6分)
∴EF,CD1共面,即E,F,C,D1四点共面,
故D1E与CF共面.…(8分)
(2)依题意可知,
最多能盛水的容积等于三棱锥C1-B1D1C的体积…(10分)
∴V=
×
×1×1×1=
.…(12分)
 解:(1)如图,连结EF,CD1,A1B,
解:(1)如图,连结EF,CD1,A1B,∵E、F分别是A1B1、BB1的中点,∴EF∥A1B,…(2分)
∵A1D1
| ∥ |
. |
| ∥ |
. |
| ∥ |
. |
∴A1D1CB是平行四边形,∴A1B∥CD1,…(4分)
∴EF∥CD1,…(6分)
∴EF,CD1共面,即E,F,C,D1四点共面,
故D1E与CF共面.…(8分)
(2)依题意可知,
最多能盛水的容积等于三棱锥C1-B1D1C的体积…(10分)
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查两直线是否共面的判断,考查容器最多能盛多少体积的水的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
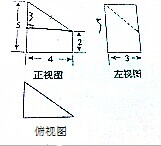 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A、54 | B、60 | C、66 | D、72 |
 阅读如图所示的程序框图,若输入的n是50,则输出的变量S的值是
阅读如图所示的程序框图,若输入的n是50,则输出的变量S的值是 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为