题目内容
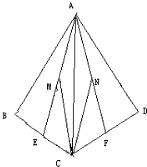 如图,在四面体ABCD中,M、N分别是△ABC和△ACD的重心,求证:
如图,在四面体ABCD中,M、N分别是△ABC和△ACD的重心,求证:(1)MN∥平面ABD;
(2)若BD⊥DC,MN⊥AD,则BD⊥AC.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由已知M,N是AE,AF的三等分点,得到AM:AE=AN:AF=2:3,得到MN∥EF,所以MN∥BD.利用线面平行的判定定理可证;
(2)由MN⊥AD,得到BD⊥AD,结合BD⊥DC,利用线面垂直的判定定理可得BD⊥平面ADC,所以BD⊥AC.
(2)由MN⊥AD,得到BD⊥AD,结合BD⊥DC,利用线面垂直的判定定理可得BD⊥平面ADC,所以BD⊥AC.
解答:
证明:(1)∵M,N分别是△ABC和△ACD的重心,
∴AM:AE=AN:AC=2:3,
∴MN∥EF,又E,F时BC,CD的中点,
∴EF∥BD,
∴MN∥BD,又MN?平面ABD,BD?平面ABD,
∴MN∥平面ABD;
(2)由(1)知MN∥BD,又MN⊥AD,
∴BD⊥AD,又BD⊥DC,AD∩DC=D
∴BD⊥平面ADC,
∴BD⊥AC.
∴AM:AE=AN:AC=2:3,
∴MN∥EF,又E,F时BC,CD的中点,
∴EF∥BD,
∴MN∥BD,又MN?平面ABD,BD?平面ABD,
∴MN∥平面ABD;
(2)由(1)知MN∥BD,又MN⊥AD,
∴BD⊥AD,又BD⊥DC,AD∩DC=D
∴BD⊥平面ADC,
∴BD⊥AC.
点评:本题考查了线面平行的判定和线面垂直的判定定理和性质定理的运用,关键时将所证转化为线线关系解决,属于常规题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
若不等式x2-
x≥0对任意实数x都成立,则实数a的取值是( )
| a |
| A、{0} | B、{0,1} |
| C、(0,1) | D、[0,+∞) |
已知在某班有
的学生数学成绩优秀,如果从班中随机地找出5名学生,那么其中数学成绩优秀的学生X~B(5,
),则E(-X)的值为( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为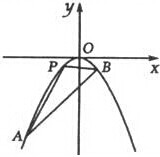 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,