题目内容
已知F1,F2分别是双曲线
-
=1(a>0,b>0)的两个焦点,点P是双曲线上的一点,且满足∠F1PF2=90°.若△PF1F2的面积为4,且双曲线的离心率为
,则双曲线的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线的定义||PF1|-|PF2||=2a,设双曲线的焦距为2c,通过|PF1|2+|PF2|2=|F1F2|2=4c2,结合△PF1F2的面积以及双曲线的离心率即可求解实轴长度.
解答:
解:由条件可得||PF1|-|PF2||=2a,由题意可知△F1PF2为直角三角形,
设双曲线的焦距为2c,则|PF1|2+|PF2|2=|F1F2|2=4c2,
故(|PF1|-|PF2|)2+2|PF1|•|PF2|=|F1F2|2=4c2,即4a2+2|PF1|•|PF2|=4c2,
故|PF1|•|PF2|=2c2-2a2=2b2,故△PF1F2的面积为
|PF1|•|PF2|=b2=4,再由双曲线的离心率e=
=
,故c=
a,故b2=c2-a2=2a2=4,即a=
,故实轴为2a=2
.
故选:C.
设双曲线的焦距为2c,则|PF1|2+|PF2|2=|F1F2|2=4c2,
故(|PF1|-|PF2|)2+2|PF1|•|PF2|=|F1F2|2=4c2,即4a2+2|PF1|•|PF2|=4c2,
故|PF1|•|PF2|=2c2-2a2=2b2,故△PF1F2的面积为
| 1 |
| 2 |
| c |
| a |
| 3 |
| 3 |
| 2 |
| 2 |
故选:C.
点评:本题考查双曲线的基本性质的应用,考查计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知数列{an}满足:a1=a2-2a+2,an+1=an+2(n-a)+1,n∈N+,当且仅当n=3时an最小,则实数a的取值范围为 ( )
| A、(-1,3) | ||||
B、(
| ||||
| C、(2,4) | ||||
D、(
|
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
=a,
=b,则
等于( )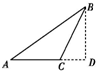
| AB |
| AC |
| BD |

A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=ax3+cx+5,已知f(-3)=3,则f(3)等于( )
| A、3 | B、-3 | C、2 | D、7 |
 阅读如图所示的程序框图,若输入的n是50,则输出的变量S的值是
阅读如图所示的程序框图,若输入的n是50,则输出的变量S的值是 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,试确定m,使得直线AP与平面BDD1B1所成角的正切值为