题目内容
已知函数f（x）在R上可导，且（x-1）•f′（x）＞0，则下列结论正确的是（ ）
| A、x=1一定是函数f（x）的极大值点 |
| B、x=1一定是函数f（x）的极小值点 |
| C、x=1不是函数f（x）的极值点 |
| D、x=1不一定是函数f（x）的极值点 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：由条件判断函数的单调性，根据函数极值和导数之间的关系即可得到结论
解答：
解：由（x-1）•f′（x）＞0得当x＞1时，f′（x）＞0，此时函数单调递增，
当x＜1时，f′（x）＜0，此时函数单调递减，
即x=1时，函数f（x）取得极小值，
故选：B．
当x＜1时，f′（x）＜0，此时函数单调递减，
即x=1时，函数f（x）取得极小值，
故选：B．
点评：本题主要考查函数极值的判断，根据函数导数和单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，若S9=72，则a1+a5+a9=（ ）
| A、36 | B、24 | C、16 | D、8 |
黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形，现将一粒豆子随机撒在第10个图中，则豆子落在白色地砖上的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
F1，F2是椭圆
+
=1（a＞b＞0）的左、右焦点，若在椭圆上存在点P，且满足|PF1|=2|PF2|，则椭圆的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、（
| ||
C、（
| ||
D、（0，
|
有甲、乙两位射击运动员进行射击测试，每人各射击10次，图1、图2分别是甲、乙两人射击命中环数分布的条形图，由条形图判断下列命题正确的是（ ）| A、总体上甲比乙的射击命中能力更强，但乙的稳定性更好 |
| B、总体上乙比甲的射击命中能力更强，但甲的稳定性更好 |
| C、总体上甲、乙两人的射击命中能力基本相当，但乙的稳定性更好 |
| D、总体上甲、乙两人的射击命中能力基本相当，但甲的稳定性更好 |
数列{an}满足a1=
，an+1=1-
，那么a10=（ ）
| 1 |
| 2 |
| 1 |
| an |
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
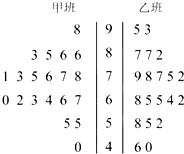某次月考从甲、乙两班中各抽取20个物理成绩，整理数据得到茎叶图如图所示，根据茎叶图解决下列问题．