题目内容
为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个2×2列联表:
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩手机游戏 | 18 | 2 | |
| 不喜欢玩手机游戏 | 6 | ||
| 合计 | 30 |
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
考点:独立性检验的应用,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(Ⅰ)根据所给数据,画出列联表;
(Ⅱ)根据公式,求出这组数据的观测值,把观测值同临界值进行比较,即可得到结论;
(Ⅲ)认为作业不多的人数为ξ,则P(ξ≥2)=P(ξ=2)+P(ξ=3).
(Ⅱ)根据公式,求出这组数据的观测值,把观测值同临界值进行比较,即可得到结论;
(Ⅲ)认为作业不多的人数为ξ,则P(ξ≥2)=P(ξ=2)+P(ξ=3).
解答:
解:(Ⅰ)根据题中所给数据,得到如下列联表:
(Ⅱ)K2=
≈8.52>7.879,
∴在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系;
(Ⅲ)认为作业不多的人数为ξ,则
P(ξ≥2)=P(ξ=2)+P(ξ=3)=
+
=
.
| 认为作业多 | 认为作业不多 | 总 计 | |
| 喜欢玩电脑游戏 | 18 | 2 | 20 |
| 不喜欢玩电脑游戏 | 4 | 6 | 10 |
| 总 计 | 22 | 8 | 30 |
| 30×(8×6-2×4)2 |
| 20×10×22×8 |
∴在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系;
(Ⅲ)认为作业不多的人数为ξ,则
P(ξ≥2)=P(ξ=2)+P(ξ=3)=
| ||||
|
| ||
|
| 2 |
| 3 |
点评:本题考查独立性检验的应用,考查概率的计算,解题的关键是利用列联表正确的计算出观测值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知随机变量X~N(1,σ2),若P(X<2)=0.8,则P(0<X<1)=( )
| A、0.6 | B、0.4 |
| C、0.3 | D、0.2 |
已知函数f(x)在R上可导,且(x-1)•f′(x)>0,则下列结论正确的是( )
| A、x=1一定是函数f(x)的极大值点 |
| B、x=1一定是函数f(x)的极小值点 |
| C、x=1不是函数f(x)的极值点 |
| D、x=1不一定是函数f(x)的极值点 |
已知p:x=2,q:0<x<3,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分,又不必要条件 |
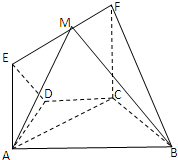 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.