题目内容
数列{an}满足a1=
,an+1=1-
,那么a10=( )
| 1 |
| 2 |
| 1 |
| an |
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据数列的递推关系得到数列是周期数列,即可得到结论.
解答:
解:∵a1=
,an+1=1-
,
∴a2=1-2=-1,a3=1+1=2,a4=1-
=
,
故数列{an}是周期数列,周期是3,
则a10=a3×3+1=a1=
,
故选:B
| 1 |
| 2 |
| 1 |
| an |
∴a2=1-2=-1,a3=1+1=2,a4=1-
| 1 |
| 2 |
| 1 |
| 2 |
故数列{an}是周期数列,周期是3,
则a10=a3×3+1=a1=
| 1 |
| 2 |
故选:B
点评:本题主要考查递推数列的应用,根据条件求出数列是周期数列是解决本题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
函数f(x)=sin(2x+
),则f′(
)的值为( )
| π |
| 6 |
| 5π |
| 12 |
| A、1 | B、-2 | C、2 | D、-1 |
在区间[-
,
]上随机取一个数x,则事件“0≤sinx≤1”发生的概率为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)在R上可导,且(x-1)•f′(x)>0,则下列结论正确的是( )
| A、x=1一定是函数f(x)的极大值点 |
| B、x=1一定是函数f(x)的极小值点 |
| C、x=1不是函数f(x)的极值点 |
| D、x=1不一定是函数f(x)的极值点 |
cos9°cos36°-sin36°sin9°的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知p:x=2,q:0<x<3,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分,又不必要条件 |
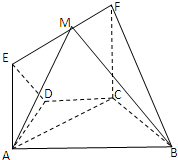 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.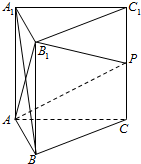 如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.
如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.