题目内容
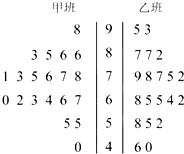 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.(1)分别指出甲乙两班物理样本成绩的中位数;
(2)分别求甲乙两班物理样板成绩的平均值;
(3)定义成绩在80分以上为优秀,现从甲乙两班物理样本成绩中有放回地各随机抽取两次,每次抽取1个成绩,设ξ表示抽出的成绩中优秀的个数,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,茎叶图,众数、中位数、平均数
专题:概率与统计
分析:(1)由茎叶图能求出甲乙两班物理样本成绩的中位数.
(2)利用平均数计算公式能求出甲乙两班物理样板成绩的平均值.
(3)甲、乙两班各有5个优秀成绩,从甲班中抽取一个成绩是优秀的概率是
,从乙班中抽取一个成绩是优秀的概率是
.由题意知ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
(2)利用平均数计算公式能求出甲乙两班物理样板成绩的平均值.
(3)甲、乙两班各有5个优秀成绩,从甲班中抽取一个成绩是优秀的概率是
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:(1)由茎叶图知:
甲乙两班物理样本成绩的中位数分别是72,70.
(2)
=
(90+80×4+70×6+60×6+50×2+40+90)=71(分),
=
(90×2+80×3+70×5+60×5+50×3+40×2+100)=70(分),
∴甲乙两班物理样板成绩的平均值分别是71分、70分.
(3)由题意知ξ的可能取值为0,1,2,3,4,
甲、乙两班各有5个优秀成绩,
∴从甲班中抽取一个成绩是优秀的概率是
,
从乙班中抽取一个成绩是优秀的概率是
,
P(ξ=0)=(
)4=
,
P(ξ=1)=2
(
)(
)3=
,
P(ξ=2)=2•(
)2(
)2+
(
)2(
)2=
,
P(ξ=3)=2
(
)2
•
•
=
,
P(ξ=4)=(
)4=
.
∴ξ的分布列为:
Eξ=0×
+1×
+2×
+3×
+4×
=1.
甲乙两班物理样本成绩的中位数分别是72,70.
(2)
. |
| x甲 |
| 1 |
| 20 |
. |
| x乙 |
| 1 |
| 20 |
∴甲乙两班物理样板成绩的平均值分别是71分、70分.
(3)由题意知ξ的可能取值为0,1,2,3,4,
甲、乙两班各有5个优秀成绩,
∴从甲班中抽取一个成绩是优秀的概率是
| 1 |
| 4 |
从乙班中抽取一个成绩是优秀的概率是
| 1 |
| 4 |
P(ξ=0)=(
| 3 |
| 4 |
| 81 |
| 256 |
P(ξ=1)=2
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 64 |
P(ξ=2)=2•(
| 1 |
| 4 |
| 3 |
| 4 |
| C | 1 2 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 128 |
P(ξ=3)=2
| C | 2 2 |
| 1 |
| 4 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 64 |
P(ξ=4)=(
| 1 |
| 4 |
| 1 |
| 256 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 81 |
| 256 |
| 27 |
| 64 |
| 27 |
| 128 |
| 3 |
| 64 |
| 1 |
| 256 |
点评:本题考查中位数、平均数的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
已知函数f(x)在R上可导,且(x-1)•f′(x)>0,则下列结论正确的是( )
| A、x=1一定是函数f(x)的极大值点 |
| B、x=1一定是函数f(x)的极小值点 |
| C、x=1不是函数f(x)的极值点 |
| D、x=1不一定是函数f(x)的极值点 |
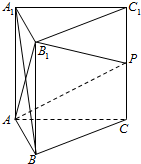 如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.
如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.