题目内容
已知直角三角形的三边分别为3cm,4cm,5cm,绕边长为4cm的边旋转一周形成一个几何体,想象并写出它是什么几何体,画出它的三视图(尺寸不作严格要求),求出它的表面积和体积.
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:直角三角形的三边分别为3cm,4cm,5cm,绕边长为4cm的边旋转一周形成的几何体是圆锥,且圆锥的高为4,底面圆的半径为3,母线长为5,画出其直观图,把数据代入面积与体积公式计算.
解答:
解:直角三角形的三边分别为3cm,4cm,5cm,绕边长为4cm的边旋转一周形成的几何体是圆锥,
且圆锥的高为4,底面圆的半径为3,母线长为5,其三视图如图:

∴圆锥的表面积S=πr(r+l)=24π(cm2),
体积V=
×π×32×4=12π(cm3).
且圆锥的高为4,底面圆的半径为3,母线长为5,其三视图如图:

∴圆锥的表面积S=πr(r+l)=24π(cm2),
体积V=
| 1 |
| 3 |
点评:本题考查了由旋转母体求几何体的表面积与体积,考查了三视图的定义,解题的关键是旋转母体判断几何体的形状及相关几何量的数据.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若曲线y=x4的一条切线l与直线x+4y-3=0垂直,则l的方程为( )
| A、4x-y-3=0 |
| B、x+4y-5=0 |
| C、4x-y+3=0 |
| D、x+4y+3=0 |
 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3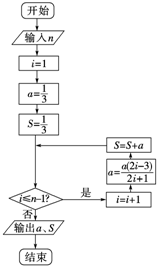 先阅读如图框图,再解答有关问题:
先阅读如图框图,再解答有关问题: