Question

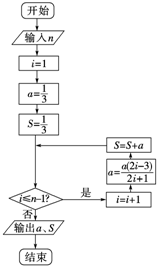先阅读如图框图，再解答有关问题：
（Ⅰ）当输入的n分别为1，2，3时，a各是多少？
（Ⅱ）当输入已知量n时，①输出a的结果是什么？试用含有n的式子表示出来；
                    ②输出S的结果是什么？写出求S的过程．

Answer 1

考点：程序框图

专题：点列、递归数列与数学归纳法,算法和程序框图

分析：（I）根据程序框图的流程，分别代入n=1，2，3．计算a值．
（II）①由框图知a_n=

2n-3

2n+1

a_n-1（n≥2），又a₁=

1

3

，利用逐积法求得a_n；②由a_n=

1

4n2-1

=

1

2

（

1

2n-1

-

1

2n+1

），又输出S的结果为数列{a_n}的前n项和为S_n，用裂项相消法求和，可得答案．

解答： 解：（I）当n=1时，a=

1

3

；
当n=2时，a=

1 3 ×(2×2-3)

5

=

1

15

；当n=3时，a=

1 15 ×(2×3-3)

2×3+1

=

1

35

．
（II）①记输入n时，输出a的结果为a_n，
则a₁=

1

3

，a_n=

2n-3

2n+1

a_n-1（n≥2），∴

an

an-1

=

2n-3

2n+1

（n≥2）．
∴a_n=

an

an-1

•

an-1

an-2

…

a2

a1

•a₁=

2n-3

2n+1

•

2n-5

2n-1

•

2n-7

2n-3

…

1

5

•

1

3

=

1

2n+1

•

1

2n-1

=

1

4n2-1

．
②输出S的结果为数列{a_n}的前n项和为S_n，
由①知，a_n=

1

4n2-1

=

1

2

（

1

2n-1

-

1

2n+1

），
∴S_n=a₁+a₂+…+a_n
=

1

2

（1-

1

3

）+

1

2

（

1

3

-

1

5

）+…+

1

2

（

1

2n-1

-

1

2n+1

）=

1

2

（1-

1

2n+1

）=

n

2n+1

．

点评：本题借助考查程序框图，主要考查了由递推关系求数列的通项公式及裂项相消法求数列的和，考查了学生的逻辑推理能力与运算能力．