题目内容
已知在△ABC中，∠B=30°，b=6，c=6
，求a及△ABC的面积S．
| 3 |
考点：正弦定理
专题：解三角形
分析：由条件利用余弦定理求得a的值，再根据S=
ac•sinB 求得△ABC的面积S．
| 1 |
| 2 |
解答：
解：在△ABC中，∵∠B=30°，b=6，c=6
，
由余弦定理可得b2=a2+c2-2ac•cosB，即 36=a2+108-12
a×
，
解得 a=12，或a=6．
当a=12时，S=
ac•sinB=18
；
当a=6时，S=
ac•sinB=9
．
| 3 |
由余弦定理可得b2=a2+c2-2ac•cosB，即 36=a2+108-12
| 3 |
| ||
| 2 |
解得 a=12，或a=6．
当a=12时，S=
| 1 |
| 2 |
| 3 |
当a=6时，S=
| 1 |
| 2 |
| 3 |
点评：本题主要考查两角和差的正弦、余弦公式的应用，属于中档题．
练习册系列答案
相关题目
设函数f（x）=lg（1-x）的定义域为A，值域为B，则A∩B=（ ）
| A、（0，+∞） |
| B、（1，+∞） |
| C、（0，1） |
| D、（-∞，1） |
已知f(x-
)=x2+
，则f（-1）=（ ）
| 1 |
| x |
| 1 |
| x2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、2 |
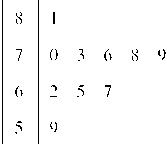已知某单位有50名职工，现要从中抽取10名职工，将全体职工随机按1～50编号，并按编号顺序平均分成10组进行系统抽样．