题目内容
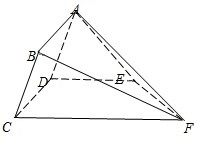 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3| 2 |
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)求直线AF与平面CDEF所成角的正切值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件,利用直线与平面、平面与平面的位置关系先推导出平面BCF∥平面ADF,由此能证明BF∥平面ADE.
(Ⅱ)由已知条件推导出面ADE⊥面CDEF,所以∠ADE就是二面角A-CD-F的平面角,为60°,作AO⊥DE于O,则AO⊥平面CDEF,连接OF,则∠AFO就是直线AF与平面CDEF所成角,由此能求出直线AF与平面CDEF所成角的正切值.
(Ⅱ)由已知条件推导出面ADE⊥面CDEF,所以∠ADE就是二面角A-CD-F的平面角,为60°,作AO⊥DE于O,则AO⊥平面CDEF,连接OF,则∠AFO就是直线AF与平面CDEF所成角,由此能求出直线AF与平面CDEF所成角的正切值.
解答:
解:(Ⅰ)因为ABCD是矩形,所以BC∥AD,
又因为BC不包含于平面ADE,
所以BC∥平面ADE,
因为DE∥CF,CF不包含于平面ADE,
所以CF∥平面ADE,
又因为BC∩CF=C,所以平面BCF∥平面ADF,
而BF?平面BCF,所以BF∥平面ADE.…(5分)
(Ⅱ)因为
⇒CD⊥面ADE,
又因为CD?面CDEF,
所以面ADE⊥面CDEF,…(10分)
因为CD⊥AD,CD⊥DE,
所以∠ADE就是二面角A-CD-F的平面角,为60°,…(11分)
因为平面CDEF⊥平面ADE,
作AO⊥DE于O,则AO⊥平面CDEF,连接OF,
所以∠AFO就是直线AF与平面CDEF所成角θ…(12分)
在Rt△AOD中,∵AD=2,∠ADE=60°,∴AO=
,
在直角梯形CDEF,
∵EF=3
,CF=6,∠CFE=45°,
∴2CD2=18,∴CD=3,
∴OF=
=
,
所以tanθ=
=
,
所以直线AF与平面CDEF所成角的正切值为
.…(15分)
又因为BC不包含于平面ADE,
所以BC∥平面ADE,
因为DE∥CF,CF不包含于平面ADE,
所以CF∥平面ADE,
又因为BC∩CF=C,所以平面BCF∥平面ADF,
而BF?平面BCF,所以BF∥平面ADE.…(5分)
(Ⅱ)因为
|
又因为CD?面CDEF,
所以面ADE⊥面CDEF,…(10分)
因为CD⊥AD,CD⊥DE,
所以∠ADE就是二面角A-CD-F的平面角,为60°,…(11分)
因为平面CDEF⊥平面ADE,
作AO⊥DE于O,则AO⊥平面CDEF,连接OF,
所以∠AFO就是直线AF与平面CDEF所成角θ…(12分)
在Rt△AOD中,∵AD=2,∠ADE=60°,∴AO=
| 3 |
在直角梯形CDEF,
∵EF=3
| 2 |
∴2CD2=18,∴CD=3,
∴OF=
| 32+(6-1)2 |
| 34 |
所以tanθ=
| AO |
| OF |
| ||
| 34 |
所以直线AF与平面CDEF所成角的正切值为
| ||
| 34 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成的角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知命题p:?a∈R,且a>0,有a+
≥2,命题q:?x∈R,sinx+cosx=
,则下列判断正确的是( )
| 1 |
| a |
| 3 |
| A、p是假命题 |
| B、q是真命题 |
| C、p∧(¬q)是真命题 |
| D、(¬p)∧q是真命题 |