题目内容
(1)求函数y=
的定义域;
(2)求函数y=sin x-
在[
,
]的最大值和最小值.
sinx-
|
(2)求函数y=sin x-
| 1 |
| 2 |
| π |
| 4 |
| 7π |
| 6 |
考点:函数的定义域及其求法,三角函数的最值
专题:函数的性质及应用,三角函数的图像与性质
分析:(1)根据函数成立的条件即可求函数y=
的定义域;
(2)根据正弦函数的性质即可求出函数的最值.
sinx-
|
(2)根据正弦函数的性质即可求出函数的最值.
解答:
解:(1)要使函数有意义,则sinx-
≥0,
即sin?x≥
,
∴2kπ+
≤x≤2kπ+
,
即函数的定义域为[2kπ+
,2kπ+
],k∈Z.
(2)∵x∈[
,
],
∴当x=
时,函数y=sin x-
取得最大值1-
=
,
当x=
时,函数y=sin x-
取得最小值sin
-
=-
-
=-1.
| ||
| 2 |
即sin?x≥
| ||
| 2 |
∴2kπ+
| π |
| 4 |
| 3π |
| 4 |
即函数的定义域为[2kπ+
| π |
| 4 |
| 3π |
| 4 |
(2)∵x∈[
| π |
| 4 |
| 7π |
| 6 |
∴当x=
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=
| 7π |
| 6 |
| 1 |
| 2 |
| 7π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数定义域和最值的求法,利用三角函数的图象和性质是解决本题的关键,比较基础.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知f(x-
)=x2+
,则f(-1)=( )
| 1 |
| x |
| 1 |
| x2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、2 |
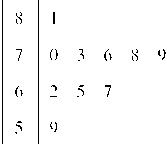 已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.