题目内容
已知数列{an}满足an+1-an=n+2(n∈N*)且a1=1
(1)求a2,a3,a4的值;
(2)求{an}的通项公式;
(3)令bn=4an-68n,求bn的最小值及此时n的值.
(1)求a2,a3,a4的值;
(2)求{an}的通项公式;
(3)令bn=4an-68n,求bn的最小值及此时n的值.
考点:数列递推式
专题:计算题,点列、递归数列与数学归纳法
分析:(1)利用an+1-an=n+2(n∈N*)且a1=1,代入计算,可得a2,a3,a4的值;
(2)由已知递推公式可利用叠加法求解数列的通项公式;
(3)将{an}的通项公式代入,利用配方法,可求bn的最小值及此时n的值.
(2)由已知递推公式可利用叠加法求解数列的通项公式;
(3)将{an}的通项公式代入,利用配方法,可求bn的最小值及此时n的值.
解答:
解:(1)∵an+1-an=n+2(n∈N*)且a1=1,
∴a2=4,a3=8,a4=13;
(2)∵an+1-an=n+2
∴a2-a1=1+2
a3-a2=2+2
…
an-an-1=(n-1)+2
以上n-1个式子相加可得,an-a1=1+2+…+(n-1)+2n-2=
;
(3)bn=4an-68n=2(n2+3n-2)-68n=2(n-
)2-
,
∴n=15或16时,bn的最小值为-484.
∴a2=4,a3=8,a4=13;
(2)∵an+1-an=n+2
∴a2-a1=1+2
a3-a2=2+2
…
an-an-1=(n-1)+2
以上n-1个式子相加可得,an-a1=1+2+…+(n-1)+2n-2=
| n2+3n-2 |
| 2 |
(3)bn=4an-68n=2(n2+3n-2)-68n=2(n-
| 31 |
| 2 |
| 953 |
| 2 |
∴n=15或16时,bn的最小值为-484.
点评:本题考查了利用递推公式求数列的通项公式,考查了累加法,考查配方法的应用,属于中档题.

练习册系列答案
相关题目
设函数f(x)=lg(1-x)的定义域为A,值域为B,则A∩B=( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、(0,1) |
| D、(-∞,1) |
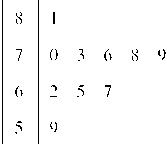 已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.