题目内容
5.设D是函数y=f(x)定义域的一个子集,若存在x0∈D,使得f(x0)=-x0成立,则称x0是f(x)的一个“准不动点”,也称f(x)在区间D上存在准不动点.已知$f(x)={log_{\frac{1}{2}}}({{4^x}+a•{2^x}-1}),x∈[{0,1}]$.(1)若a=1,求函数f(x)的准不动点;
(2)若函数f(x)在区间[0,1]上存在准不动点,求实数a的取值范围.
分析 (1)由题意,当a=1时,可得f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+{2}^{x}-1)=-x$,x∈[0,1],可得函数f(x)的准不动点.
(2)依题意,“f(x)在区间D上有不动点”当且仅当“F(x)=f(x)+x在区间D上有零点”,F(x)在区间[0,1]上是一条连续不断的曲线,换元法转化为二次函数问题求解准不动点,可得实数a的取值范围.
解答 解:(1)由题意,当a=1时,可得f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+{2}^{x}-1)=-x$,x∈[0,1],
可得:4x+2x-1=2x,
即4x=1
∴x=0.
当a=1,函数f(x)的准不动点为x0=0.
(2)由定义:f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+a{2}^{x}-1)=-x$,x∈[0,1],上有零点”,
可得:F(x)=4x+a•2x-1-2x,即F(x)=(2x)2+a•2x-1-2x,上有零点”,
且4x+a•2x-1>0,
令2x=t,
x∈[0,1],
则t∈[1,2]
那么F(x)转化为g(x)=t2+at-t-1,上有零点”图象是一条连续不断的曲线,
且t2+at-1>0,(1≤t≤2).
根据二次函数根的分布:则有$\left\{\begin{array}{l}{g(1)≤0}\\{g(2)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{g(1)≥0}\\{g(2)≤0}\end{array}\right.$.
解得$-\frac{1}{2}≤a≤1$.
要使t2+at-1>0(1≤t≤2)恒成立.
其对称轴x=$-\frac{a}{2}$,在1≤t≤2上是递增的,当t=1时最小值,
可得a>0.
综上可得实数a的取值范围是(0,1].
点评 本题主要考查了函数与方程的综合运用,以及函数零点最值等有关知识,属于中档题.

| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
| A. | p1+p2+p3 | B. | 1-(1-p1)(1-p2)(1-p3) | C. | 1-p1p2p3 | D. | p1p2p3 |
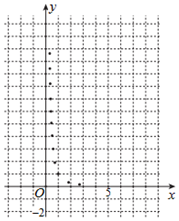 某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).| $\bar x$ | $\bar y$ | $\bar w$ | $\sum_{i=1}^{10}{({x_i}-\bar x)^2}$ | $\sum_{i=1}^{10}{({w_i}-\bar w)^2}$ | $\sum_{i=1}^{10}({x_i}-\bar x)({y_i}-\bar y)$ | $\sum_{i=1}^{10}({w_i}-\bar w)({y_i}-\bar y)$ |
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
(1)根据散点图判断,y=a+bx与$y=c+\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立y关于x的回归方程;
(3)若旋转的弧度数x与单位时间内煤气输出量t成正比,那么x为多少时,烧开一壶水最省煤气?
附:对于一组数据(u1,v1),(u2,v2),(u3,v3),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\hat β=\frac{{\sum_{i=1}^n{({v_i}-\bar v)({u_i}-\bar u)}}}{{\sum_{i=1}^n{{{({u_i}-\bar u)}^2}}}},\hat α=\bar v-\hat β\bar u$.
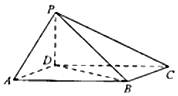 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.