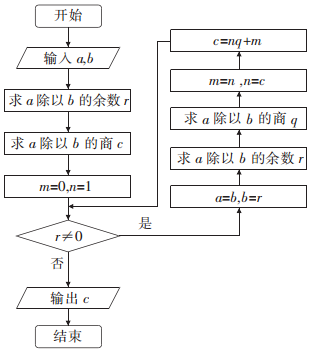
题目内容
16.在区间[-1,1]上任取两数a、b,则关于x的二次方程x2+2ax+b=0有两个实数根的概率为( )| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
分析 由二次方程x2+2ax+b=0有两个实数根列出a,b满足的条件,再在坐标系aob中画出区域,利用定积分求出面积,由测度比为面积比得答案.
解答 解:由题意可得$\left\{\begin{array}{l}{-1≤a≤1}\\{-1≤b≤1}\\{4{a}^{2}-4b≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{-1≤a≤1}\\{-1≤b≤1}\\{b≤{a}^{2}}\end{array}\right.$.
画出图形如图: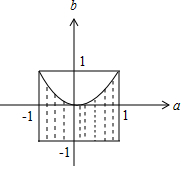
图中阴影部分的面积为S=${∫}_{-1}^{1}({a}^{2}+1)da=(\frac{1}{3}{a}^{3}+a){|}_{-1}^{1}$=$\frac{8}{3}$.
∴关于x的二次方程x2+2ax+b=0有两个实数根的概率为$\frac{\frac{8}{3}}{4}=\frac{2}{3}$.
故选:D.
点评 本题主要考查了几何概型,以及一元二次方程的根的分布与系数的关系,属于基础题.

练习册系列答案
相关题目
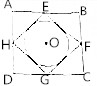 已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.
已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.