题目内容
10.设$f(x)=lg({\frac{2}{1-x}+a})$是奇函数,则使f(x)>1的x的取值范围是$({\frac{9}{11}.1})$.分析 根据若f(x)是奇函数且在x=0有定义,则f(0)=0,即可解出a.再根据对数函数的单调性解不等式得到答案.
解答 解:依题意,得f(0)=0,即lg(2+a)=0,
所以,a=-1,f(x)=lg $\frac{1+x}{1-x}$,
由f(x)>1,得lg $\frac{1+x}{1-x}$>1,
故$\frac{1+x}{1-x}$>10,解得:$\frac{9}{11}$<x<1,
故答案为:$({\frac{9}{11}.1})$.
点评 题主要考查函数的奇偶性和对数不等式的解法.在解对数不等式时注意对数函数的单调性,即:底数大于1时单调递增,底数大于0小于1时单调递减.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
20.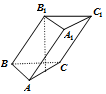 已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
 已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
19.已知命题p:f(x)=lnx+2x2+6mx+1在(0,+∞)上单调递增,q:m≥-5,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
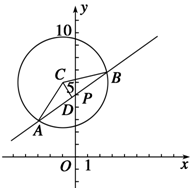 已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.
已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.