Question

13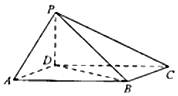．如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ）证明：PA⊥BD；
（II）若PD=AD，求AD与平面PAB所成角的正弦值．

Answer 1

分析 （Ⅰ）证明PA⊥BD，只需证明BD⊥平面PAD，即需证明BD⊥AD，BD⊥PD；
（Ⅱ）以D为坐标原点，射线DA为x轴的正半轴建立空间直角坐标系D-xyz，则A（1，0，0），B（0，$\sqrt{3}$，0），P（0，0，1）．C（-1，$\sqrt{3}$，0），D（0，0，0），利用向量求解．

解答 解：令AB=2AD=2，
（Ⅰ）证明：因为∠DAB=60°，AB=2AD=2，
由余弦定理得DB=$\sqrt{3}$，从而BD²+AD²=AB²，故BD⊥AD，
又PD⊥底面ABCD，BD?底面ABCD，∴BD⊥PD，
∵AD∩PD=D，∴BD⊥平面PAD，
∵PA?平面PAD，∴PA⊥BD．
（Ⅱ） 如图，以D为坐标原点，射线DA为x轴的正半轴建立空间直角坐标系D-xyz，
则A（1，0，0），B（0，$\sqrt{3}$，0），P（0，0，1）．C（-1，$\sqrt{3}$，0），D（0，0，0），
则$\overrightarrow{AD}=（-1，0，0）$，$\overrightarrow{AB}=（-1，\sqrt{3}，0）$，$\overrightarrow{PB}=（0，\sqrt{3}，-1）$，
设平面PAB的法向量为$\overrightarrow{n}$=（x，y，z），则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=-x+\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{3}y-z=0}\end{array}\right.$，
因此可取$\overrightarrow{n}=（\sqrt{3}，1，\sqrt{3}$），
cos＜$\overrightarrow{AD}$，$\overrightarrow{n}$＞=-$\frac{\sqrt{21}}{7}$，
∴AD与平面PAB所成角的正弦值为$\frac{\sqrt{21}}{7}$

点评 本题考查线线垂直，考查线面角，解题的关键是掌握线面垂直的判定与性质，正确运用向量求线面角，属于中档题．