Question

15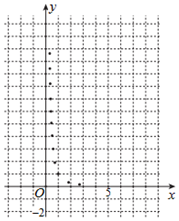．某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据，且作了一定的数据处理（如表），得到了散点图（如图）．

$\bar x$	$\bar y$	$\bar w$	$\sum_{i=1}^{10}{（{x_i}-\bar x）^2}$	$\sum_{i=1}^{10}{（{w_i}-\bar w）^2}$	$\sum_{i=1}^{10}（{x_i}-\bar x）（{y_i}-\bar y）$	$\sum_{i=1}^{10}（{w_i}-\bar w）（{y_i}-\bar y）$
1.47	20.6	0.78	2.35	0.81	-19.3	16.2

表中${w_i}=\frac{1}{x_i^2}，\overline{w}=\frac{1}{10}\sum_{i=1}^{10}{w_i}$．
（1）根据散点图判断，y=a+bx与$y=c+\frac{d}{x^2}$哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立y关于x的回归方程；
（3）若旋转的弧度数x与单位时间内煤气输出量t成正比，那么x为多少时，烧开一壶水最省煤气？
附：对于一组数据（u₁，v₁），（u₂，v₂），（u₃，v₃），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\hat β=\frac{{\sum_{i=1}^n{（{v_i}-\bar v）（{u_i}-\bar u）}}}{{\sum_{i=1}^n{{{（{u_i}-\bar u）}^2}}}}，\hat α=\bar v-\hat β\bar u$．

Answer 1

分析 （1）根据散点图是否按直线型分布作答；
（2）根据回归系数公式得出y关于ω的线性回归方程，再得出y关于x的回归方程；
（3）利用基本不等式得出煤气用量的最小值及其成立的条件．

解答 解：（1）$y=c+\frac{d}{x^2}$更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型．…（1分）
（2）由公式可得：$\hat d=\frac{{\sum_{i=1}^{10}{（{w_i}-\bar w）（{y_i}-\bar y）}}}{{\sum_{i=1}^{10}{{{（{w_i}-\bar w）}^2}}}}=\frac{16.2}{0.81}=20$，…（3分）
$\hat c=\bar y-\hat d\overline{w}=20.6-20×0.78=5$，…（5分）
所以所求回归方程为$y=5+\frac{20}{x^2}$．…（6分）
（3）设t=kx，则煤气用量$S=yt=kx（5+\frac{20}{x^2}）=5kx+\frac{20k}{x}≥2\sqrt{5kx•\frac{20k}{x}}=20k$，…（9分）
当且仅当$5kx=\frac{20k}{x}$时取“=”，即x=2时，煤气用量最小．…（11分）
答：x为2时，烧开一壶水最省煤气．                            …（12分）

点评 本题考查了可化为线性相关的回归方程的求解，基本不等式的应用，属于中档题．