题目内容
1．定义在R上的偶函数f（x），当x≥0时，f（x）=x2+log2（x+1），若f（t）≥f（2），则t的取值范围是（ ）| A． | （-∞，-2] | B． | [2，+∞） | C． | [-2，2] | D． | （-∞，-2]∪[2，+∞） |
分析 根据函数奇偶性的性质结合函数单调性进行转化求解即可．
解答 解：当x≥0时，f（x）=x2+log2（x+1）为增函数，
∵f（x）是偶函数，
∴不等式f（t）≥f（2），等价为f（|t|）≥f（2），
即|t|≥2，
即t≥或t≤-2，
即t的取值范围是（-∞，-2]∪[2，+∞），
故选：D．
点评 本题主要考查函数奇偶性和单调性的应用，利用奇偶性和单调性的关系将不等式进行转化是解决本题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
11．
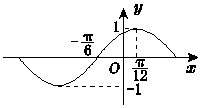已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）
已知函数f（x）=Asin（ωx+φ）（A、ω＞0）的图象如图所示，则其解析式可以是（ ）| A． | $y=sin（{x+\frac{π}{6}}）$ | B． | $y=sin（{x+\frac{π}{3}}）$ | C． | $y=sin（{2x-\frac{2π}{3}}）$ | D． | $y=sin（{2x+\frac{π}{3}}）$ |
6．从一批苹果中随机抽取100个作为样本，其重量（单位：克）的频数分布表如下：
（1）在频率分布直方图中，求分组重量在[85，95）对应小矩形的高；
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．
| 分组（重量） | [75，85） | [85，95） | [95，105） | [105，115） |
| 频数（个） | 15 | 30 | 35 | 20 |
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．
10．设扇形的半径长为2cm，面积为4cm2，则扇形的圆心角的弧度数是（ ）
| A． | 1 | B． | 2 | C． | π | D． | $\frac{5}{6}$ |