题目内容
11.已知函数f(x)=ax2+xlnx+x.(1)若a=1,求函数f(x)在(1,f(1))处的切线方程;
(2))若a=-e,证明:方程$|{f(x)}|-lnx=\frac{1}{2}x$无解.
分析 (1)求得a=1时f(x)的导数,求出切线的斜率和切点坐标,由点斜式方程即可得到所求切线方程;
(2)由题意可得|-ex+lnx+1|=$\frac{lnx}{x}$+$\frac{1}{2}$,设g(x)=-ex+lnx+1,求得导数和单调区间,可得g(x)>1;设h(x)=$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,+∞),求得导数,单调区间,可得h(x)max=h(e)=$\frac{lne}{e}$+$\frac{1}{2}$=$\frac{1}{e}$+$\frac{1}{2}$<1,即可得证.
解答 (1)解:依题意,函数f(x)=x2+xlnx+x,
f′(x)=2x+lnx+2,…(2分)
故f′(1)=2+ln1+2=4,f(1)=1+ln1+1=2,
则函数f(x)在(1,f(1))处的切线方程为y-2=4(x-1),
即y=4x-2.…(4分)
(2)证明:依题意,|-ex2+xlnx+x|=lnx+$\frac{1}{2}$x,即|-ex+lnx+1|=$\frac{lnx}{x}$+$\frac{1}{2}$.
设g(x)=-ex+lnx+1,g′(x)=$\frac{-ex+1}{x}$,
g(x)在(0,$\frac{1}{e}$)上递增,在($\frac{1}{e}$,+∞)上递减,
∴g(x)max=g($\frac{1}{e}$)=-e•$\frac{1}{e}$+ln$\frac{1}{e}$+1=-1,
∴g(x)max=g($\frac{1}{e}$)=-1,
∴g(x)<-1.…(8分)
设h(x)=$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,+∞)
则h′(x)=$\frac{1-lnx}{{x}^{2}}$.
h(x)在(0,e)上递增,在(e,+∞)上递减,
h(x)max=h(e)=$\frac{lne}{e}$+$\frac{1}{2}$=$\frac{1}{e}$+$\frac{1}{2}$<1,
即|g(x)|>h(x),
故方程$|{f(x)}|-lnx=\frac{1}{2}x$无解.…(12分)
点评 本题考查导数的运用:求切线方程和单调区间、最值,考查函数方程的转化思想,以及构造函数法,考查化简整理的运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
α的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
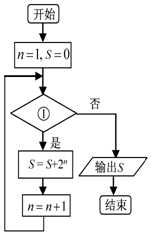
| A. | n≤5 | B. | n≤6 | C. | n≤7 | D. | n≤8 |
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
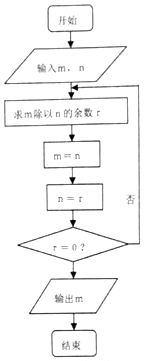 如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入m,n分别为225、135,则输出的m=( )
如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入m,n分别为225、135,则输出的m=( )