题目内容
11.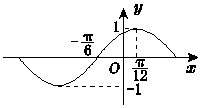 已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A、ω>0)的图象如图所示,则其解析式可以是( )| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=sin({x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{2π}{3}})$ | D. | $y=sin({2x+\frac{π}{3}})$ |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:根据函数f(x)=Asin(ωx+φ)(A、ω>0)的图象,可得A=1,$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{π}{12}$+$\frac{π}{6}$,∴ω=2.
再根据五点法作图可得2•$\frac{π}{12}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{3}$,∴f(x)=sin(2x+$\frac{π}{3}$),
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
16.直线x+y-2=0和x-y-4=0的交点为( )
| A. | (3,-1) | B. | (-3,-1) | C. | (-3,1) | D. | (3,1) |
3.已知实数x,y满足2x+y+10=0,那么$\sqrt{{x^2}+{y^2}}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{10}$ |
20.己知函数f(x)=x3-3x,若过点A(1,m)可作曲线y=f(x)的三条切线,则实数m的取值范围是( )
| A. | -1<m<1 | B. | -4<m<4 | C. | -1<m<-2 | D. | -3<m<-2 |
1.定义在R上的偶函数f(x),当x≥0时,f(x)=x2+log2(x+1),若f(t)≥f(2),则t的取值范围是( )
| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |