题目内容
10.设扇形的半径长为2cm,面积为4cm2,则扇形的圆心角的弧度数是( )| A. | 1 | B. | 2 | C. | π | D. | $\frac{5}{6}$ |
分析 设扇形的弧长为2,根据扇形的半径和面积,利用扇形面积公式列式算出l=4,再由弧度的定义加以计算,即可得到该扇形的圆心角的弧度数.
解答 解:设扇形的圆心角的弧度数是α,弧长为l,
∵扇形的半径长r=2cm,面积S=4cm2,
∴S=$\frac{1}{2}$lr,即4=$\frac{1}{2}$×l×2,解之得l=4,
因此,扇形圆心角的弧度数是α=$\frac{l}{r}$=$\frac{4}{2}$=2.
故选:B.
点评 本题给出扇形的半径和面积,求圆心角的大小.考查了扇形的面积公式和弧度制的定义等知识,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
20.己知函数f(x)=x3-3x,若过点A(1,m)可作曲线y=f(x)的三条切线,则实数m的取值范围是( )
| A. | -1<m<1 | B. | -4<m<4 | C. | -1<m<-2 | D. | -3<m<-2 |
1.定义在R上的偶函数f(x),当x≥0时,f(x)=x2+log2(x+1),若f(t)≥f(2),则t的取值范围是( )
| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
19.若平面α的一个法向量为$\overrightarrow{n}$=(0,2,2),A(1,0,2),B(0,-1,4),A∉α,B∈α,则点A到平面
α的距离为( )
α的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
2.某学校对手工社、摄影社两个社团招新报名的情况进行调查,得到如下的2×2列联表:
(1)请填上上表中所空缺的五个数字;
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
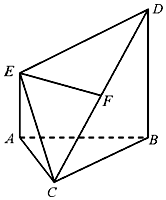 如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.