题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x>1}\\{{x}^{2}-3,x≤1}\end{array}\right.$,若关于x的方程f(x)=$\frac{a}{x}$恰有两个不同解,则实数a的取值范围为[-2,0]∪{2}.分析 分类讨论,利用关于x的方程f(x)=$\frac{a}{x}$恰有两个不同解,即可求出实数a的取值范围.
解答 解:由题意,a>0,x>1时,lnx=$\frac{a}{x}$有一个解;
x≤1时,x2-3=$\frac{a}{x}$只有一个解,即a=x3-3x只有一个解,
令y=x3-3x,则y′=3(x+1)(x-1),
∴x<-1时,y′>0,-1<x<1时,y′<0,
x=-1时,y=2,x=1时,y=-2,此时a=2满足题意;
同理,-2≤a≤0满足题意,
故答案为[-2,0]∪{2}.
点评 本题考查函数与方程的应用,利用条件转化为两个函数的交点个数问题是解决本题的关键.

练习册系列答案
相关题目
3.已知实数x,y满足2x+y+10=0,那么$\sqrt{{x^2}+{y^2}}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{10}$ |
1.定义在R上的偶函数f(x),当x≥0时,f(x)=x2+log2(x+1),若f(t)≥f(2),则t的取值范围是( )
| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
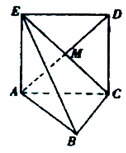 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC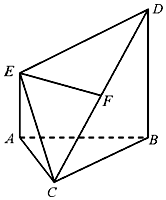 如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.