题目内容
2.向量$\overrightarrow{a}$、$\overrightarrow{b}$均为非零向量,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$\overrightarrow{a}$、$\overrightarrow{b}$不是共线向量,求证:($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$).分析 由题意易证明($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,可得垂直.
解答 证明:∵向量$\overrightarrow{a}$、$\overrightarrow{b}$均为非零向量,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$\overrightarrow{a}$、$\overrightarrow{b}$不是共线向量,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-${\overrightarrow{b}}^{2}$=|$\overrightarrow{a}$|2=|$\overrightarrow{b}$|2=0,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$).
点评 本题考查向量的数量积和垂直关系,属基础题.

练习册系列答案
相关题目
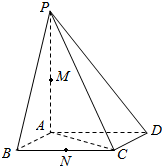 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.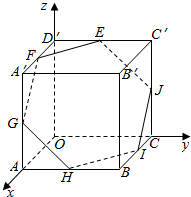 正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.