题目内容
11.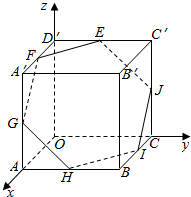 正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
分析 根据正方体各棱长相等,结合中点坐标公式,即可求出六边形各顶点的坐标.
解答 解:正方体OABC-D′A′B′C′的棱长为a,
且E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,
∴正六边形EFGHIJ各顶点的坐际为E(0,$\frac{a}{2}$,a),F($\frac{a}{2}$,0,a),
G(a,0,$\frac{a}{2}$),H(a,$\frac{a}{2}$,0),I($\frac{a}{2}$,a,0),J(0,a,$\frac{a}{2}$).
点评 本题考查了空间直角坐标系与正方体的应用问题,是基础题目.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
16.已知点A的坐标为(2,3),F为抛物线y2=2x的焦点,若点P在抛物线上移动,当|PF|-|PA|取得最大值,则点P的坐标是( )
| A. | (2,2) | B. | ($\sqrt{6}$,3) | C. | (3,$\sqrt{6}$) | D. | ($\frac{9}{2}$,3) |
20.已知函数f(x)=a|x|(a>0,a≠1)在区间(-∞,0)上为增函数,且对任意x∈[m,m+1],不等式f(x+m)≤f2(x)恒成立,则实数m的取值范围是( )
| A. | m≤-$\frac{3}{2}$ | B. | m≤-3 | C. | m≤-$\frac{2}{3}$ | D. | m≤-$\frac{3}{4}$ |
4.不等式$\frac{2-3x}{x-1}>0$的解集为( )
| A. | $(-∞,\frac{3}{4})$ | B. | $(-∞,\frac{2}{3})$ | C. | $(-∞,\frac{2}{3})∪(1,+∞)$ | D. | $(\frac{2}{3},1)$ |