题目内容
13.$\underset{lim}{n→∞}$$\frac{1+2n+3{n}^{2}+…+2004{n}^{2003}}{{n}^{2003}+2{n}^{2002}+…+2003n+2004}$=2004.分析 将原式的分子分母同时除以n2003得$\frac{\frac{1}{{n}^{2003}}+\frac{2}{{n}^{2002}}+\frac{3}{{n}^{2001}}+…+\frac{1}{{n}^{0}}•2004}{1+\frac{2}{n}+\frac{3}{{n}^{2}}+…+\frac{2004}{{n}^{2003}}}$,再直接取其极限即可.
解答 解:将原式的分子分母同时除以n2003,
原式=$\underset{lim}{n→∞}$$\frac{1+2n+3{n}^{2}+…+2004{n}^{2003}}{{n}^{2003}+2{n}^{2002}+…+2003n+2004}$
=$\underset{lim}{n→∞}$$\frac{\frac{1}{{n}^{2003}}+\frac{2}{{n}^{2002}}+\frac{3}{{n}^{2001}}+…+\frac{1}{{n}^{0}}•2004}{1+\frac{2}{n}+\frac{3}{{n}^{2}}+…+\frac{2004}{{n}^{2003}}}$,
其中,$\underset{lim}{n→∞}$$\frac{1}{{n}^{k}}$=0,k=1,2,3,…,2003,
所以,原式=$\frac{0+0+0+…+0+2004}{1+0+0+…+0+0}$=2004.
故答案为:2004.
点评 本题主要考查了数列极限及其运算,将分式的分子分母同时除以n的最高次数项是解决本题的关键,属于中档题.

练习册系列答案
相关题目
3.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=x+x3 | B. | y=3x | C. | y=log2x | D. | $y=-\frac{1}{x}$ |
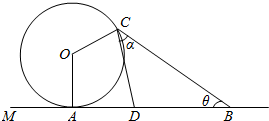 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.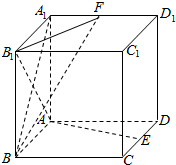 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点. 试根据流程图回答:
试根据流程图回答: