题目内容
17．若f（x）=ln（$\sqrt{{4x}^{2}+1}$-2x）-1．则f（x）+f（-x）=（ ）| A． | -2 | B． | 0 | C． | 1 |
分析 写出f（x）+f（-x）=$ln（\sqrt{4{x}^{2}+1}-2x）+ln（\sqrt{4{x}^{2}+1}+2x）$-2，进行对数的运算即可得出答案．
解答 解：$f（x）+f（-x）=ln（\sqrt{4{x}^{2}+1}-2x）$$+ln（\sqrt{4{x}^{2}+1}+2x）-2$=ln1-2=-2．
故选A．
点评 考查对数的运算，以及平方差公式的运用．
练习册系列答案
阅读快车系列答案
相关题目
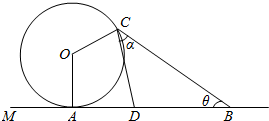如图，在一条景观道的一端有一个半径为50米的圆形摩天轮O，逆时针15分钟转一圈，从A处进入摩天轮的座舱，OA垂直于地面AM，在距离A处150米处设置了一个望远镜B．
试根据流程图回答：
7．已知sinα+$\sqrt{3}$cosα=2，则tanα=（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |