题目内容
10.己知向量$\overrightarrow{a}$=(2cosx,-1),$\overrightarrow{b}$=(2sin(x+$\frac{π}{6}$),1),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(1)求f(x)的解析表达式;
(2)求f(x)的最小正周期;
(3)求f(x)在区间[-$\frac{π}{6}$,$\frac{π}{4}$]上的值域.
分析 (1)由数量积和三角函数公式化简可得f(x)=2sin(2x+$\frac{π}{6}$);
(2)由周期公式可得;
(3)由x∈[-$\frac{π}{6}$,$\frac{π}{4}$]可得三角函数函数的值域.
解答 解:(1)∵$\overrightarrow{a}$=(2cosx,-1),$\overrightarrow{b}$=(2sin(x+$\frac{π}{6}$),1),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=4cosxsin(x+$\frac{π}{6}$)-1=4cosx($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)-1
=2$\sqrt{3}$sinxcosx+2cos2x-1=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$)
∴f(x)的解析表达式为f(x)=2sin(2x+$\frac{π}{6}$);
(2)由(1)可得f(x)的最小正周期T=$\frac{2π}{2}$=π;
(3)∵x∈[-$\frac{π}{6}$,$\frac{π}{4}$],∴2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],∴2sin(2x+$\frac{π}{6}$)∈[-1,2],
∴函数的值域为:[-1,2]
点评 本题考查两角和与差的三角函数公式,涉及数量积的运算,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知函数f(x)=a|x|(a>0,a≠1)在区间(-∞,0)上为增函数,且对任意x∈[m,m+1],不等式f(x+m)≤f2(x)恒成立,则实数m的取值范围是( )
| A. | m≤-$\frac{3}{2}$ | B. | m≤-3 | C. | m≤-$\frac{2}{3}$ | D. | m≤-$\frac{3}{4}$ |
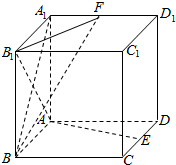 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点. 试根据流程图回答:
试根据流程图回答: