题目内容
设函数f(θ)=
sinθ+cosθ,其中θ的顶点与坐标原点重合,始终与x轴非负半轴重合,终边经过点P(x,y)且0≤θ≤π.
(1)若点P的坐标为(
,
),则f(θ)的值为
(2)若点P(x,y)为平面区域Ω:
内的一个动点,记f(θ)的最大值为M,最小值m,则logMm= .
| 3 |
(1)若点P的坐标为(
| 1 |
| 2 |
| ||
| 2 |
(2)若点P(x,y)为平面区域Ω:
|
考点:两角和与差的正弦函数,任意角的三角函数的定义,正弦函数的定义域和值域
专题:计算题,三角函数的求值
分析:首先由两角和的正弦公式,化简f(θ).
(1)由P的坐标为(
,
),则θ=
,代入,即可得到;
(2)画出平面区域Ω,由图象得到0≤θ≤
,即有
≤θ+
≤
,再由正弦函数的性质即可得到最值.
(1)由P的坐标为(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
(2)画出平面区域Ω,由图象得到0≤θ≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
解答:
解:f(θ)=
sinθ+cosθ=2(
sinθ+
cosθ)=2sin(θ+
).
(1)由P的坐标为(
,
),则θ=
,f(θ)=2sin(
+
)=2sin
=2;
(2)平面区域Ω:
如图: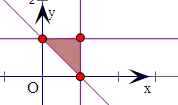
则P位于点(0,1)处,θ最大,位于点(1,0)处最小,即0≤θ≤
,
即有
≤θ+
≤
,
则f(θ)的最大值为M=f(
)=2,最小值为m=f(0)=1,
则logMm=log21=0.
故答案为:2,0.
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(1)由P的坐标为(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(2)平面区域Ω:
|

则P位于点(0,1)处,θ最大,位于点(1,0)处最小,即0≤θ≤
| π |
| 2 |
即有
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
则f(θ)的最大值为M=f(
| π |
| 3 |
则logMm=log21=0.
故答案为:2,0.
点评:本题考查三角函数的化简和求值,考查不等式组表示的平面区域,考查正弦函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f(x)的定义域为[2,16],则y=f(x)+f(2x)的定义域为( )
| A、[2,16] |
| B、[1,8] |
| C、[1,16] |
| D、[2,8] |
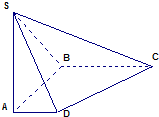 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<