题目内容
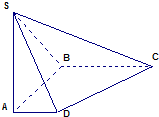 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<| DS |
| DB |
| 1 |
| 5 |
(Ⅰ)求直线BS与平面SCD所成角的正弦值;
(Ⅱ)求面SAB与面SCD所成二面角的正弦值.
考点:二面角的平面角及求法,直线与平面所成的角
专题:空间角
分析:(Ⅰ)设SA=m,由已知得4+m2=1+m2+5-2
×
×
,从而得m=2,以A为原点建立如图所示的空间直角坐标系A-xyz,利用向量法能求出直线BS与平面SCD所成角的正弦值.
(Ⅱ)求出平面SAB的法向量,利用向量法能求出平面SAB与面SCD所成的二面角的正弦值.
| m2+1 |
| 5 |
| 1 |
| 5 |
(Ⅱ)求出平面SAB的法向量,利用向量法能求出平面SAB与面SCD所成的二面角的正弦值.
解答:
解:(Ⅰ)设SA=m,∵SA2=DS2+DB2-2DS•DBcos<
,
>,
∴4+m2=1+m2+5-2
×
×
,
解得m=2,
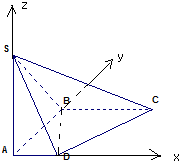
以A为原点建立如图所示的空间直角坐标系A-xyz,
则D(1,0,0),C(2,2,0),S(0,0,2),B(0,2,0),
=(0,-2,2),
=(1,2,0),
=(-1,0,2),
设平面SCD的法向量为
=(x,y,z),
则
,
令z=1,则
=(2,-1,1),
设直线BS与平面SCD所成角为θ,
则sinθ=
=
=
.
(Ⅱ)∵SA⊥底面ABCD,AD⊥AB,
∴平面SAB的法向量为
=(1,0,0),
cos<
,
>=
=
,
平面SAB与面SCD所成的二面角的正弦值为
=
.
| DS |
| DB |
∴4+m2=1+m2+5-2
| m2+1 |
| 5 |
| 1 |
| 5 |

解得m=2,
以A为原点建立如图所示的空间直角坐标系A-xyz,
则D(1,0,0),C(2,2,0),S(0,0,2),B(0,2,0),
| BS |
| DC |
| DS |
设平面SCD的法向量为
| m |
则
|
令z=1,则
| m |
设直线BS与平面SCD所成角为θ,
则sinθ=
|
| ||||
|
|
| 0+2+2 | ||||
|
| ||
| 3 |
(Ⅱ)∵SA⊥底面ABCD,AD⊥AB,
∴平面SAB的法向量为
| AD |
cos<
| AD |
| m |
| ||||
|
|
| ||
| 3 |
平面SAB与面SCD所成的二面角的正弦值为
1-(
|
| ||
| 3 |
点评:本题考查直线BS与平面SCD所成角的正弦值的求法,考查面SAB与面SCD所成二面角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知:集合P={x|x≤3},则( )
| A、-2⊆P | B、{-2}∈P |
| C、{-2}⊆P | D、∅∈P |
一直异面直线a,b分别在α,β内,面α∩β=c,则直线c( )
| A、一定与a,b中的两条都相交 |
| B、至少与a,b中的一条平行 |
| C、至多与a,b中的一条相交 |
| D、至少与a,b中的一条相交 |
已知锐角α,β满足sinα=
,cosβ=
,则α+β=( )
| ||
| 5 |
3
| ||
| 10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|