题目内容
16.数列{an}的前n项和记为Sn,a1=10,an+1=2Sn+1(n≥1)(1)求{an}的通项公式;
(2)求Sn.
分析 (1)利用数列递推关系、等比数列的定义及其通项公式即可得出.
(2)由an+1=2Sn+1(n≥1),可得:Sn=$\frac{{a}_{n+1}-1}{2}$.
解答 解:(1)由an+1=2Sn+1可得an=2Sn-1+1(n≥2),
两式相减得an+1-an=2an,an+1=3an(n≥2),
又a2=2S1+1=3,∴a2=3a1,
∴{an}是首项为1,公比为3得等比数列,
∴an=3n-1.
(2)由an+1=2Sn+1(n≥1),
可得:Sn=$\frac{{a}_{n+1}-1}{2}$=$\frac{{3}^{n}-1}{2}$.
点评 本题考查了数列递推关系、等比数列的定义及其通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.若等差数列{an}满足a1+a2+a2015+a2016=3,则{an}的前2016项之和S2016=( )
| A. | 1506 | B. | 1508 | C. | 1510 | D. | 1512 |
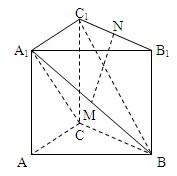 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.