题目内容
6.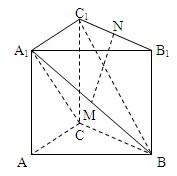 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别是A1B、B1C1的中点.(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成角的大小;
(3)求二面角A-BC-A1的平面的余弦值;
(4)求点B1到平面A1BC的距离.
分析 (1)由BC⊥AC,BC⊥CC1,则BC⊥平面ACC1A1,连接AC1,则BC⊥AC1.侧面ACC1A1是正方形,所以A1C⊥AC1.又BC∩A1C=C,根据线面垂直的判定定理可知AC1⊥平面A1BC,因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点,又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1,从而MN⊥平面A1BC;
(2)根据AC1⊥平面A1BC,设AC1与A1C相交于点D,连接BD,根据线面所成角的定义可知∠C1BD为直线BC1和平面A1BC所成角,设AC=BC=CC1=a,求出C1D,BC1,在Rt△BDC1中,求出∠C1BD,即可求出所求.
(3)由题意,∠A1CA为二面角A-BC-A1的平面角;
(4)由等体积可得点B1到平面A1BC的距离.
解答 (1)证明:由已知BC⊥AC,BC⊥CC1,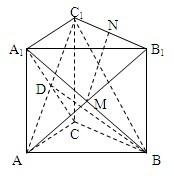
所以BC⊥平面ACC1A1.连接AC1,则BC⊥AC1.
由已知,侧面ACC1A1是矩形,所以A1C⊥AC1.
又BC∩A1C=C,所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.
故MN⊥平面A1BC.
(2)解:因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连接BD,则∠C1BD为直线BC1和平面A1BC所成角.
设AC=BC=CC1=a,则C1D=$\frac{\sqrt{2}}{2}$a,BC1=$\sqrt{2}$a.
在Rt△BDC1中,sin∠C1BD=$\frac{1}{2}$,
所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
(3)解:由题意,∠A1CA为二面角A-BC-A1的平面角,
由于AC=BC=CC1=a,∴cos∠A1CA=$\frac{\sqrt{2}}{2}$,
∴二面角A-BC-A1的平面角的余弦值为$\frac{\sqrt{2}}{2}$;
(4)解:设点B1到平面A1BC的距离为h,则由等体积可得$\frac{1}{3}×\frac{1}{2}a•\sqrt{2}a•h=\frac{1}{3}×\frac{1}{2}a•\sqrt{2}a•\frac{\sqrt{2}}{2}a$,
∴$h=\frac{\sqrt{2}}{2}a$.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面所成角、二面角的度量,考查点到平面距离的计算,同时考查了化归与转化的数学思想方法,以及空间想象能力、运算求解能力和推理论证能力,属于中档题.

 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |
| A. | 垂直 | B. | 长度相等 | C. | 异面 | D. | 夹角为60° |
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| A. | 抽签法 | B. | 分层抽样法 | C. | 系统抽样法 | D. | 随机数法 |