题目内容
设f(x)满足f(-sinx)+3f(sinx)=4sinx•cosx(|x|≤
).
(1)求f(x)的解析式;
(2)求f(x)的最大值.
| π |
| 2 |
(1)求f(x)的解析式;
(2)求f(x)的最大值.
考点:函数的最值及其几何意义,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题(1)要求函数的解析式,先将x用“-x”替换,得到关于“sinx”的关系式,再利用换元法得到函数f(x)的解析式;(2)利用基本不等式可以求出函数的最大值.
解答:
解:(1)∵f(-sinx)+3f(sinx)=4sinx•cosx(|x|≤
). ①
∴将x用“-x”代入,得到:
f[-sin(-x)]+3f[sin(-x)]=4sin(-x)•cos(-x),
即f(sinx)+3f(-sinx)=-4sinx•cosx.②
再将①×3-②得:
8f(sinx)=16sinx•cosx,
f(sinx)=2sinx•cosx.
∵|x|≤
,
∴cosx=
.
∴f(sinx)=2sinx
.
令sinx=t,则有:f(t)=2t
, t∈[-1,1].
即f(x)=2x
, x∈[-1,1].
(2)∵2ab≤a2+b2(a>0,b>0),
∴当x>0时,2x
≤x2+(1-x2)=1,
当且仅当x=
,即x=
时取等号.
∵
∈[-1,1],
∴可以取到最大值.
∴f(x)的最大值为1.
| π |
| 2 |
∴将x用“-x”代入,得到:
f[-sin(-x)]+3f[sin(-x)]=4sin(-x)•cos(-x),
即f(sinx)+3f(-sinx)=-4sinx•cosx.②
再将①×3-②得:
8f(sinx)=16sinx•cosx,
f(sinx)=2sinx•cosx.
∵|x|≤
| π |
| 2 |
∴cosx=
| 1-sin2x |
∴f(sinx)=2sinx
| 1-sin2x |
令sinx=t,则有:f(t)=2t
| 1-t2 |
即f(x)=2x
| 1-x2 |
(2)∵2ab≤a2+b2(a>0,b>0),
∴当x>0时,2x
| 1-x2 |
当且仅当x=
| 1-x2 |
| ||
| 2 |
∵
| ||
| 2 |
∴可以取到最大值.
∴f(x)的最大值为1.
点评:本题考查了函数的解析式和最值的求法,利用函数方程思想和换元法求函数的解析式,利用基本不等式求函数的最值,注意不等式取等号的条件.本题有一定的综合性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC中,点D在BC边上,且
=4
=r
+s
,则3r+s=( )
| CD |
| DB |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A={x|
>1},B={x||x|<a},若∅?B⊆A,则实数a的取值范围是( )
| 4 |
| x+1 |
| A、a<1 | B、a≤1 |
| C、1≤a≤3 | D、0<a≤1 |
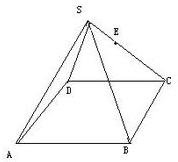 在底面是菱形的四棱锥S-ABCD中,SA=SC=2a,SB=SD=
在底面是菱形的四棱锥S-ABCD中,SA=SC=2a,SB=SD=