Question

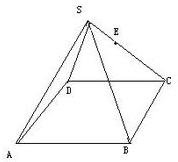在底面是菱形的四棱锥S-ABCD中，SA=SC=2a，SB=SD=

2

a，E是SC上的一点且SE=λa（0＜λ≤a），求证：对任意λ∈（0，a]，都有BD⊥AE．

Answer 1

考点：直线与平面垂直的性质

专题：空间位置关系与距离

分析：连结BD，AC交与点O，连结SO，由四边形ABCD为菱形，推断出O为AC，BD的中点，又SA=SC，SB=SD可知SO⊥AC，SO⊥BD，利用线面垂直的判定定理推断出SO⊥平面ABCD，进而利用线面垂直的性质推断出BD⊥SO，又BD⊥AC利用线面垂直的判定定理可知BD⊥平面SAC，进而根据线面垂直的性质可知BD⊥AE．

解答： 证明：连结BD，AC交与点O，连结SO，
∵四边形ABCD为菱形，
∴O为AC，BD的中点
∵SA=SC，SB=SD
∴SO⊥AC，SO⊥BD，
∵AC∩BD=O，AC?平面ABCD，BD?平面ABCD，
∴SO⊥平面ABCD，
∵BD?平面ABCD，
∴BD⊥SO，
∵BD⊥AC，AC∩SO=O，AC?平面SAC，SO?平面SAC，
∴BD⊥平面SAC，
又对任意λ∈（0，a]，AE?平面SAC，
∴BD⊥AE．

点评：本题主要考查了线面垂直的判定定理和性质的应用．考查了学生对基础定理和性质的理解和记忆．