题目内容
已知函数f(x)=2sin2x+2
sinxcosx-1
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最小值及相应x的值.
| 3 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最小值及相应x的值.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)利用二倍角的正弦、余弦公式,两角差的正弦公式,对解析式进行化简,利用周期公式求出函数的最小正周期;
(2)把“2x-
”作为一个整体,根据正弦函数的最小值和对应的x的取值,求出此函数的最值和对应的x的值.
(2)把“2x-
| π |
| 6 |
解答:
解:(1)f(x)=2sin2x+2
sinxcosx-1
=
sin2x-cos2x=2sin(2x-
),
则T=
=π,
(2)当(2x-
)=
+2kπ(k∈Z)时,
sin(2x-
)=-1,
则函数f(x)取得最小值为-2.
此时,x=
+kπ(k∈Z).
| 3 |
=
| 3 |
| π |
| 6 |
则T=
| 2π |
| 2 |
(2)当(2x-
| π |
| 6 |
| 3π |
| 2 |
sin(2x-
| π |
| 6 |
则函数f(x)取得最小值为-2.
此时,x=
| 5π |
| 6 |
点评:本题考查了二倍角的正弦、余弦公式,两角差的正弦公式,正弦函数的性质的应用,以及整体思想.

练习册系列答案
相关题目
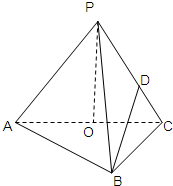 如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.