题目内容
设数列{an}的前n项和为Sn,a1=b且an=2an-1+
(n>1,n∈N*)
(Ⅰ)若b=-
,求a2,a3,a4;
(Ⅱ)若{an}是递增数列,求实数b的取值范围;
(Ⅲ)若?n∈N*,Sn≥S2恒成立,求实数b的取值范围.
| 1 |
| 2n |
(Ⅰ)若b=-
| 1 |
| 8 |
(Ⅱ)若{an}是递增数列,求实数b的取值范围;
(Ⅲ)若?n∈N*,Sn≥S2恒成立,求实数b的取值范围.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)根据b的值和递推公式,依次求出a2,a3,a4;
(Ⅱ)根据递推公式的特点,两边同乘以2n进行变形后构造数列bn=2nan,代入式子得:bn=4bn-1+1,
再设bn+k=4(bn-1+k),利用待定系数法求出k的值,构造新的等比数列{bn+
},利用等比数列,的通项公式求出bn,再求出an的表达式,利用条件得:an+1-an>0对任意n∈N*恒成立,代入后化简求出b的取值范围;
(Ⅲ)由(Ⅱ)求出的an,利用分组求和法和等比数列的前n项和公式求出Sn的表达式,再化简出Sn-S2的表达式并分离b,再对n进行分类讨论,利用恒成立求出最值方法求出对应的b的取值范围.
(Ⅱ)根据递推公式的特点,两边同乘以2n进行变形后构造数列bn=2nan,代入式子得:bn=4bn-1+1,
再设bn+k=4(bn-1+k),利用待定系数法求出k的值,构造新的等比数列{bn+
| 1 |
| 3 |
(Ⅲ)由(Ⅱ)求出的an,利用分组求和法和等比数列的前n项和公式求出Sn的表达式,再化简出Sn-S2的表达式并分离b,再对n进行分类讨论,利用恒成立求出最值方法求出对应的b的取值范围.
解答:
解:(Ⅰ)由b=-
,a1=b且an=2an-1+
(n>1,n∈N*)得,
a2=2×(-
)+
=0,a3=2×0+
=
,a4=2×
+
=
;
(Ⅱ)由an=2an-1+
得,2nan=4(2n-1an-1)+1,
令bn=2nan,则b1=2a1=b,bn=4bn-1+1,
设bn+k=4(bn-1+k),得bn=4bn-1+3k,
解得k=
,即bn+
=4(bn-1+
)
∴数列{bn+
}是以2b+
为首项、4为公比的等比数列,
∴bn+
=(2b+
)•4n-1,则bn=(2b+
)•4n-1-
,
故2nan=(2b+
)•4n-1-
,
∴an=(2b+
)•2n-2-
,
∵{an}是递增数列,∴an+1-an>0对任意n∈N*恒成立,
则an+1-an=(2b+
)•2n-1-
-((2b+
)•2n-2-
)
=(2b+
)•2n-2+
>0,
∴2b+
>-
对任意n∈N*恒成立,
又∵-
<0,
∴2b+
≥0,解得b≥-
,
(Ⅲ)由(Ⅱ)得,an=(2b+
)•2n-2-
,
∴Sn=(2b+
)•
-
•
=(b+
)•(2n-1)-
•(1-
),
∵?n∈N*,Sn≥S2恒成立,
∴(b+
)•(2n-1)-
•(1-
)≥3b+
恒成立,
即(2n-4)b≥
-
-
恒成立,
当n≥3时,由(2n-4)b≥
-
-
得,
(2n-4)b≥
-
-
=
=
化简得b≥
-
,
只要b≥
-
=-
=-
即可,
当n=2时,2n-4=0≥
-
-
=0,成立,
当n=1时,(2n-4)b≥
-
-
为-2b≥
,即b≤-
,
综上所述:实数b的取值范围是-
≤b≤-
.
| 1 |
| 8 |
| 1 |
| 2n |
a2=2×(-
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 16 |
| 5 |
| 16 |
(Ⅱ)由an=2an-1+
| 1 |
| 2n |
令bn=2nan,则b1=2a1=b,bn=4bn-1+1,
设bn+k=4(bn-1+k),得bn=4bn-1+3k,
解得k=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴数列{bn+
| 1 |
| 3 |
| 1 |
| 3 |
∴bn+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故2nan=(2b+
| 1 |
| 3 |
| 1 |
| 3 |
∴an=(2b+
| 1 |
| 3 |
| 1 |
| 3•2n |
∵{an}是递增数列,∴an+1-an>0对任意n∈N*恒成立,
则an+1-an=(2b+
| 1 |
| 3 |
| 1 |
| 3•2n+1 |
| 1 |
| 3 |
| 1 |
| 3•2n |
=(2b+
| 1 |
| 3 |
| 1 |
| 3•2n+1 |
∴2b+
| 1 |
| 3 |
| 1 |
| 3•22n-1 |
又∵-
| 1 |
| 3•22n-1 |
∴2b+
| 1 |
| 3 |
| 1 |
| 6 |
(Ⅲ)由(Ⅱ)得,an=(2b+
| 1 |
| 3 |
| 1 |
| 3•2n |
∴Sn=(2b+
| 1 |
| 3 |
| ||
| 1-2 |
| 1 |
| 3 |
| ||||
1-
|
=(b+
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2n |
∵?n∈N*,Sn≥S2恒成立,
∴(b+
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2n |
| 1 |
| 4 |
即(2n-4)b≥
| 3 |
| 4 |
| 1 |
| 3•2n |
| 2n |
| 6 |
当n≥3时,由(2n-4)b≥
| 3 |
| 4 |
| 1 |
| 3•2n |
| 2n |
| 6 |
(2n-4)b≥
| 3 |
| 4 |
| 1 |
| 3•2n |
| 2n |
| 6 |
| 9•2n-4-2•22n |
| 12•2n |
| (-2•2n+1)(2n-4) |
| 12•2n |
化简得b≥
| 1 |
| 12•2n |
| 1 |
| 6 |
只要b≥
| 1 |
| 12•23 |
| 1 |
| 6 |
| 15 |
| 96 |
| 5 |
| 32 |
当n=2时,2n-4=0≥
| 3 |
| 4 |
| 1 |
| 3•2n |
| 2n |
| 6 |
当n=1时,(2n-4)b≥
| 3 |
| 4 |
| 1 |
| 3•2n |
| 2n |
| 6 |
| 1 |
| 4 |
| 1 |
| 8 |
综上所述:实数b的取值范围是-
| 5 |
| 32 |
| 1 |
| 8 |
点评:本题考查了等比数列的定义、通项公式、前n项和公式,递推公式的转化和应用,以及分组法求数列的前n项和,构造法求数列的通项公式,分离法求参数的值,考查了分类讨论思想、转化思想和恒成立问题,难度较大,需要很强的逻辑思维能力和计算化简能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
执行如图所示的程序框图,若输出的k=6,则输入的整数p的最大值为( )
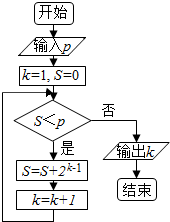

| A、7 | B、15 | C、31 | D、63 |
 如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.
如图,已知鞭形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠EFA=60°,点H,G分别是线段EF,BC的中点,点M为HE的中点.