题目内容
给出定义:若m-
<x≤m+
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个结论:
①函数y=f(x)的定义域为R,值域为[0,
];
②函数y=f(x)的图象关于直线x=
(k∈Z)对称;
③函数y=f(x)是偶函数;
④函数y=f(x)在[-
,
]上是增函数.
其中正确结论的个数是( )
| 1 |
| 2 |
| 1 |
| 2 |
①函数y=f(x)的定义域为R,值域为[0,
| 1 |
| 2 |
②函数y=f(x)的图象关于直线x=
| k |
| 2 |
③函数y=f(x)是偶函数;
④函数y=f(x)在[-
| 1 |
| 2 |
| 1 |
| 2 |
其中正确结论的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:新定义,函数的性质及应用
分析:根据让函数解析式有意义的原则确定函数的定义域,然后根据解析式易用分析法求出函数的值域;根据f(k-x)与f(-x)的关系,可以判断函数y=f(x)的图象是否关于直线x=
(k∈Z)对称;再判断f(-x)=f(x)是否成立,可以判断③的正误;而由①的结论,易判断函数y=f(x)在[-
,
]上的单调性,但要说明④不成立,我们可以举出一个反例.
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:①中,令x=m+a,a∈(-
,
],
∴f(x)=|x-{x}|=|a|∈[0,
]
故①正确;
②中∵f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(x),
所以关于x=
对称,故②正确;
③中,∵f(-x)=|(-x)-{-x}|=|x-{x}|=f(x),
所以f(x)为偶函数,故③正确;
④中,x=-
时,m=-1,f(-
)=
,x=
时,m=0,
f(
)=
所以f(-
)=f(
)故④错误.
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=|x-{x}|=|a|∈[0,
| 1 |
| 2 |
故①正确;
②中∵f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(x),
所以关于x=
| k |
| 2 |
③中,∵f(-x)=|(-x)-{-x}|=|x-{x}|=f(x),
所以f(x)为偶函数,故③正确;
④中,x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查的知识点是利用函数的三要素、性质判断命题的真假,我们要根据定义中给出的函数,结合求定义域、值域的方法,及对称性、周期性和单调性的证明方法,对4个结论进行验证.

练习册系列答案
相关题目
已知函数f(x)在R上满足f(x)=2f(-x)-x2则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、y=x |
| B、y=2x-1 |
| C、y=3x-2 |
| D、y=-2x+3 |
函数f(x)=x-
在区间(1,+∞)上是增函数,则实数p的取值范围是( )
| p |
| x |
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,+∞) |
| D、[1,+∞) |

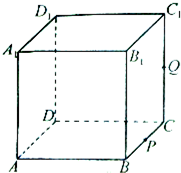 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是