��Ŀ����
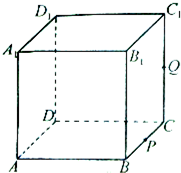 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ����
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ�����ٵ�CQ=1ʱ��S�����Ϊ
| ||
| 2 |
�ڵ�
| 3 |
| 4 |
�۵�CQ=
| 3 |
| 4 |
| 1 |
| 3 |
�ܵ�CQ=
| 1 |
| 2 |
�ݵ�0��CQ��
| 1 |
| 2 |
���㣺���������ж���Ӧ��
ר�⣺�ռ�λ�ù�ϵ�����
�������٣���CQ=1ʱ����Q���C1�غϣ���ͼ֪������SΪ���Σ����������Ϊ
�����жϢ٣�
ȡAD���е�M����DD1��ȡ��N��ʹ��DN=CQ����MN��PQ����AT��MN����ֱ��DD1�ڵ�T����A��P��Q��T�ĵ㹲�棻
�ڣ���
��CQ��1ʱ��
��DN��1⇒DT=2DN�ʣ�
��2����T��DD1���ӳ����ϣ���TQ��C1D1���ڵ�E��AT��A1D1���ڵ�F����SΪ�����APQEF�����жϢڣ�
�ۣ���CQ=
ʱ����DN=
⇒DT=2DN=
⇒D1T=
����D1R��TD1=BC��DT�����D1R=
���̶��ɵ�C1R=
�����жϢۣ�
�ܣ���CQ=
ʱ����DN=
����֪��T��D1�غϣ��Ӷ�֪SΪ��������APQD1�����жϢܣ�
�ݣ���0��CQ��
ʱ����0��DN��
⇒DT=2DN��1⇒SΪ�ı���APQT�����жϢݣ���
| ||
| 2 |
ȡAD���е�M����DD1��ȡ��N��ʹ��DN=CQ����MN��PQ����AT��MN����ֱ��DD1�ڵ�T����A��P��Q��T�ĵ㹲�棻
�ڣ���
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
�ۣ���CQ=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
�ܣ���CQ=
| 1 |
| 2 |
| 1 |
| 2 |
�ݣ���0��CQ��
| 1 |
| 2 |
| 1 |
| 2 |
���
�⣺���ڢ٣���CQ=1ʱ����Q���C1�غϣ���ʱ����A��P��Q��ƽ����A1D1�ཻ��R���ҵ�RΪA1D1���е㣬
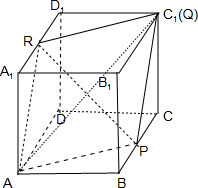
��ʱ������APQRΪ���Σ������ε������Խ��߷ֱ�Ϊ��AQ=
��PR=
��
����S=
��
��
=
���ʢ���ȷ��
ȡAD���е�M����DD1��ȡ��N��ʹ��DN=CQ����MN��PQ����AT��MN����ֱ��DD1�ڵ�T����A��P��Q��T�ĵ㹲�棻
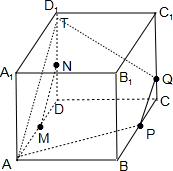
���ڢڣ���
��CQ��1ʱ��
��DN��1⇒DT=2DN�ʣ�
��2����T��DD1���ӳ����ϣ���TQ��C1D1���ڵ�E��AT��A1D1���ڵ�F����SΪ�����APQEF���ʢڴ���
���ڢۣ���CQ=
ʱ����DN=
⇒DT=2DN=
⇒D1T=
����D1R��TD1=BC��DT⇒D1R=
⇒C1R=
���ʢ���ȷ��
���ڢܣ���CQ=
ʱ����DN=
⇒DT=2DN=1⇒��T��D1�غ�⇒SΪ��������APQD1���ʢ���ȷ��
���ڢݣ���0��CQ��
ʱ����0��DN��
⇒DT=2DN��1⇒SΪ�ı���APQT���ʢ���ȷ��
���ϣ�������ȷ���ǣ��٢ۢܢݣ�
�ʴ�Ϊ���٢ۢܢݣ�

��ʱ������APQRΪ���Σ������ε������Խ��߷ֱ�Ϊ��AQ=
| 3 |
| 2 |
����S=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
ȡAD���е�M����DD1��ȡ��N��ʹ��DN=CQ����MN��PQ����AT��MN����ֱ��DD1�ڵ�T����A��P��Q��T�ĵ㹲�棻

���ڢڣ���
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
���ڢۣ���CQ=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
���ڢܣ���CQ=
| 1 |
| 2 |
| 1 |
| 2 |
���ڢݣ���0��CQ��
| 1 |
| 2 |
| 1 |
| 2 |
���ϣ�������ȷ���ǣ��٢ۢܢݣ�
�ʴ�Ϊ���٢ۢܢݣ�
���������⿼����������������⣬Ҫ��ѧ������������ķ�����Ҫ�����������ƽ�С�����ƽ�е����ʶ���ȷ�����棬�������������ʽ��о���ļ��㣬�������⣮

��ϰ��ϵ�д�
�����Ŀ
��֪����P={x|x2��4}�� Q={x|
��4}����P��Q=��������
| x |
| A��{x|x��2} | B��{x|0��x��2} |
| C��P | D��Q |
���к����мȲ����溯��Ҳ����ż�������ǣ�������
| A��y=2|x| | ||||
B��y=lg(
| ||||
| C��y=2x-2-x | ||||
D��
|
�輯��A={1��3��a}��B={1��2}��A?B����a��ֵΪ��������
| A��0 | B��1 | C��2 | D��3 |
��ֱ��mx+3y+3=0��2x+��m-1��y+2=0ƽ�У���ʵ��m��ֵΪ��������
| A��3��-2 | B��-3��2 |
| C��3 | D��-2 |