Question

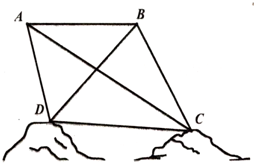为了绘制海底地图，测量海底两点C，D间的距离，海底探测仪沿水平方向在A，B两点进行测量，A，B，C，D在同一个铅垂平面内．海底探测仪测得∠BAC=30°，∠DAC=45°，∠ABD=45°，∠DBC=75°，A，B两点的距离为

3

海里．
（1）求△ABD的面积；
（2）求C，D之间的距离．

Answer 1

考点：余弦定理,解三角形的实际应用

专题：应用题,解三角形

分析：（1）易求∠ADB，在△ABD中，由正弦定理，得

BD

sin∠BAD

=

AB

sin∠ADB

，代入数值可求；
（2）可判断△ABC为等腰三角形，可求BC，△BCD中，由余弦定理可求CD．

解答： 解：（1）∠ADB=180°-30°-45°-45°=60°，
在△ABD中，由正弦定理，得

BD

sin∠BAD

=

AB

sin∠ADB

，
∴

BD

sin∠75°

=

3

sin∠60°

，解得BD=

6 + 2

2

．
∴S△ABD=

1

2

AB•BDsin∠ABD=

1

2

×

3

×

6 + 2

2

×sin45°=

3+ 3

4

．
（2）△ABC中，∠ACB=180°-30°-45°-75°=30°，
∴BC=BA=

3

，
△BCD中，由余弦定理，得CD²=BC²+BD²-2BC•BDcos∠DBC
=3+(

6 + 2

2

)2-2×

3

×

6 + 2

2

×

6 - 2

4

=5，
∴CD=

5

．

点评：该题考查正弦定理、余弦定理及其应用，考查学生对问题的阅读理解能力．