题目内容
已知函数f(x)=sin(x+
)+cos(x-
),x∈R.
(1)求f(x)的最小正周期和最值;
(2)已知cos(β-α)=
,cos(β+α)=-
,(0<α<β≤
),求证:[f(β)]2-2=0.
| 7π |
| 4 |
| 3π |
| 4 |
(1)求f(x)的最小正周期和最值;
(2)已知cos(β-α)=
| 4 |
| 5 |
| 4 |
| 5 |
| π |
| 2 |
考点:两角和与差的正弦函数,两角和与差的余弦函数,三角函数的周期性及其求法
专题:计算题,证明题,三角函数的图像与性质
分析:(1)运用两角和差的正弦和余弦公式,化简f(x)得到2sin(x-
),再求出周期和最值;
(2)运用两角和差的余弦公式,再相加即得cosβcosα=0,由0<α<β≤
得到β=
,求出f(β),即可得证.
| π |
| 4 |
(2)运用两角和差的余弦公式,再相加即得cosβcosα=0,由0<α<β≤
| π |
| 2 |
| π |
| 2 |
解答:
(1)解:函数f(x)=sin(x+
)+cos(x-
)
=sinxcos
+cosxsin
+cosxcos
+sinxsin
=
sinx-
cosx-
cosx+
sinx=
sinx-
cosx
=2sin(x-
),
∴f(x)的最小正周期为π,f(x)max=2,f(x)min=-2;
(2)证明:cos(β-α)=cosβcosα+sinβsinα=
,
cos(β+α)=cosβcosα-sinβsinα=-
,
两式相加,得cosβcosα=0,
又0<α<β≤
,
则cosα∈(0,1),cosβ=0,β=
,
f(β)=2sin
=
,
∴[f(β)]2-2=0.
| 7π |
| 4 |
| 3π |
| 4 |
=sinxcos
| 7π |
| 4 |
| 7π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
=2sin(x-
| π |
| 4 |
∴f(x)的最小正周期为π,f(x)max=2,f(x)min=-2;
(2)证明:cos(β-α)=cosβcosα+sinβsinα=
| 4 |
| 5 |
cos(β+α)=cosβcosα-sinβsinα=-
| 4 |
| 5 |
两式相加,得cosβcosα=0,
又0<α<β≤
| π |
| 2 |
则cosα∈(0,1),cosβ=0,β=
| π |
| 2 |
f(β)=2sin
| π |
| 4 |
| 2 |
∴[f(β)]2-2=0.
点评:本题主要考查两角和差的三角函数,考查三角函数的周期和最值,属于基础题.

练习册系列答案
相关题目
用反证法证明命题“已知A,B,C,D是空间中的四点,直线AB与CD是异面直线,则直线AC和BD也是异面直线.”应假设( )
| A、直线AC和BD是平行直线 |
| B、直线AB和CD是平行直线 |
| C、直线AC和BD是共面直线 |
| D、直线AB和CD是共面直线 |
计算:sin225°的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
 如图,△ABC的两边AB=2,AC=1,点D在BC边上,且满足
如图,△ABC的两边AB=2,AC=1,点D在BC边上,且满足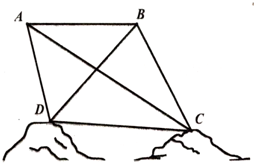 为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为
为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为