题目内容
某选手进行6次投篮训练，每次投中的概率均为p，且每次投中与否是相互独立的，记投中的次数为X，若随机变量X的数学期望EX=4．
（Ⅰ）求p的值；
（Ⅱ）若这6次投篮中有4次或者4次以上未投中，则需继续训练，求该选手需要继续训练的概率．
（Ⅰ）求p的值；
（Ⅱ）若这6次投篮中有4次或者4次以上未投中，则需继续训练，求该选手需要继续训练的概率．
考点：n次独立重复试验中恰好发生k次的概率
专题：概率与统计
分析：（1）由题意可得随机变量X服从二项分布，n=6，再由EX=6p=4，求得p的值．
（2）由条件根据n次独立重复实验中恰好发生k次的概率公式求得由于4次没有投中的概率、5次没有投中的概率、6次没有投中的概率，相加，即得所求．
（2）由条件根据n次独立重复实验中恰好发生k次的概率公式求得由于4次没有投中的概率、5次没有投中的概率、6次没有投中的概率，相加，即得所求．
解答：
解：（1）由题意可得随机变量X服从二项分布，n=6，由 EX=6p=4，求得 p=
．
（2）由于4此没有投中的概率为
•(
)4•(
)2=
，5次没有投中的概率为
•(
)5•
=
，6次没哟投中的概率为
•(
)6=
，
故至少有4次未投中的概率为
+
+
=
．
| 2 |
| 3 |
（2）由于4此没有投中的概率为
| C | 4 6 |
| 1 |
| 3 |
| 2 |
| 3 |
| 60 |
| 729 |
| C | 5 6 |
| 1 |
| 3 |
| 2 |
| 3 |
| 12 |
| 729 |
| C | 6 6 |
| 1 |
| 3 |
| 1 |
| 729 |
故至少有4次未投中的概率为
| 60 |
| 729 |
| 12 |
| 729 |
| 1 |
| 729 |
| 73 |
| 729 |
点评：本题主要考查服从二项分布的随机变量的期望，n次独立重复实验中恰好发生k次的概率，体现了分类讨论的数学额思想，属于基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
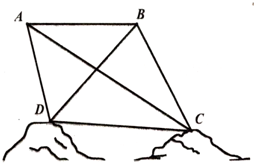为了绘制海底地图，测量海底两点C，D间的距离，海底探测仪沿水平方向在A，B两点进行测量，A，B，C，D在同一个铅垂平面内．海底探测仪测得∠BAC=30°，∠DAC=45°，∠ABD=45°，∠DBC=75°，A，B两点的距离为