题目内容

已知定义在（0，π）的函数 f（x）=sinx-
1
2
x，则f（x）的单调递减区间为（　　）
A、（0，π）
B、（0，
π
6
）
C、（
π
3
，π）
D、（
π
2
，π）
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求导数可得y′=cosx-
1
2
，令其小于0，解不等式可得答案．
解答： 解：∵y=sinx-
1
2
x，
∴y′=cosx-
1
2
，
令y′＜0，结合x∈（0，π）可得x，
故函数的单调递减区间为（
π
3
，π）
故选：C．
点评：本题考查函数的单调性，用导数工具是解决问题的关键，属基础题
练习册系列答案
相关题目
存在x∈R，使|3x+1|≤|2x|+a成立，则实数a的取值范围是
 
．
有限集合的元素可以一一数出来，无限集合的元素虽然不能数尽，但是可以比较两个集合元素个数的多少，例如，对于集合A={1，2，3，…，n，…}与B={2，4，6，…，2n，…}，我们可以设计一种方法得出A与B的元素个数一样多的结论，类似地，给出下列4组集合：
（1）A={1，2，3，…，n，…}与B={2，4，8，…，2n，…}
（2）A=[0，1]与B=[0，2]
（3）A=（0，2]与B=[-1，+∞）
（4）A={（x，y）|x2+y2=1}与B={（x，y）|
x2
4
+y2=1}
元素个数一样多的有（　　）
A、1组B、2组C、3组D、4组
用反证法证明命题“已知A，B，C，D是空间中的四点，直线AB与CD是异面直线，则直线AC和BD也是异面直线．”应假设（　　）
A、直线AC和BD是平行直线
B、直线AB和CD是平行直线
C、直线AC和BD是共面直线
D、直线AB和CD是共面直线
根据图所示的算法流程图，输出的结果T为（　　）
A、8B、48C、49D、50
向量
a
=（k，
2
），
b
=（2，-2）且
a
•
b
=-4
2
，则k的值为（　　）
A、2
B、
2
C、-2
D、-
2
一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{an}，若a8=15，且a1，a2，a5成等比数列，则此样本的平均数和中位数分别是（　　）
A、11，10
B、10，10
C、11，12
D、10，12
计算：sin225°的值为（　　）
A、
2
2
B、-
2
2
C、-
3
2
D、-
1
2
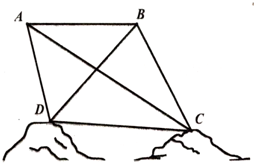为了绘制海底地图，测量海底两点C，D间的距离，海底探测仪沿水平方向在A，B两点进行测量，A，B，C，D在同一个铅垂平面内．海底探测仪测得∠BAC=30°，∠DAC=45°，∠ABD=45°，∠DBC=75°，A，B两点的距离为
3
海里．
（1）求△ABD的面积；
（2）求C，D之间的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网