题目内容
已知函数f(x)=
x2-2x(x∈R),g(x)=m+4ln(x+1)(-1<x≤4).
(Ⅰ)求f(x)在x=1处的切线方程;
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且仅有两个不同的交点?若存在,求出m的值或范围;若不存在,说明理由.
| 1 |
| 2 |
(Ⅰ)求f(x)在x=1处的切线方程;
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且仅有两个不同的交点?若存在,求出m的值或范围;若不存在,说明理由.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(Ⅰ)求出导数,求出切线的斜率和切点坐标,应用点斜式方程写出切线方程;
(Ⅱ)遇到关于两个函数的图象的交点个数的问题,一般是构造新函数,题目转化为研究函数的零点问题,通过导数得到函数的最值,把函数的最值同0进行比较,得到结果.
(Ⅱ)遇到关于两个函数的图象的交点个数的问题,一般是构造新函数,题目转化为研究函数的零点问题,通过导数得到函数的最值,把函数的最值同0进行比较,得到结果.
解答:
解:(Ⅰ)函数f(x)=
x2-2x的导数f′(x)=x-2,
则切线的斜率为1-2=-1,切点为(1,-
),
∴f(x)在x=1处的切线方程为:y+
=-(x-1)即2x+2y+1=0;
(Ⅱ)函数y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点,
即函数m(x)=f(x)-g(x)的图象与x轴(-1<x≤4)有且只有两个不同的交点.
∵m(x)=
x2-2x-4ln(x+1)-m,m′(x)=
(-1<x≤4)
当x∈(-1,3)时,m'(x)<0,m(x)是减函数;
当x∈(3,4)时,m'(x)>0,m(x)是增函数;
∴m(x)极小值=m(3)=-m-8ln2-
.
又m(4)=-4ln5,
∴要使函数m(x)=f(x)-g(x)的图象与x轴(-1<x≤4)有且只有两个不同的交点,
必须且只须m(4)>0且m(3)<0,
即-8ln2-
<m<-4ln5.
∴存在实数m,使得函数y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点,
且m的取值范围为(-8ln2-
,-4ln5).
| 1 |
| 2 |
则切线的斜率为1-2=-1,切点为(1,-
| 3 |
| 2 |
∴f(x)在x=1处的切线方程为:y+
| 3 |
| 2 |
(Ⅱ)函数y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点,
即函数m(x)=f(x)-g(x)的图象与x轴(-1<x≤4)有且只有两个不同的交点.
∵m(x)=
| 1 |
| 2 |
| (x-3)(x+2) |
| x+1 |
当x∈(-1,3)时,m'(x)<0,m(x)是减函数;
当x∈(3,4)时,m'(x)>0,m(x)是增函数;
∴m(x)极小值=m(3)=-m-8ln2-
| 3 |
| 2 |
又m(4)=-4ln5,
∴要使函数m(x)=f(x)-g(x)的图象与x轴(-1<x≤4)有且只有两个不同的交点,
必须且只须m(4)>0且m(3)<0,
即-8ln2-
| 3 |
| 2 |
∴存在实数m,使得函数y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点,
且m的取值范围为(-8ln2-
| 3 |
| 2 |
点评:本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力.

练习册系列答案
相关题目
向量
=(k,
),
=(2,-2)且
•
=-4
,则k的值为( )
| a |
| 2 |
| b |
| a |
| b |
| 2 |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
 如图,△ABC的两边AB=2,AC=1,点D在BC边上,且满足
如图,△ABC的两边AB=2,AC=1,点D在BC边上,且满足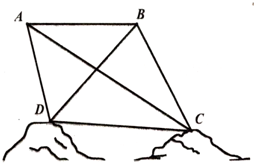 为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为
为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为