题目内容
已知集合A={x|x2-2x-a2-2a<0},B={y|y=3x-2a,x≤2}.
(Ⅰ)若a=3,求A∪B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
(Ⅰ)若a=3,求A∪B;
(Ⅱ)若A∩B=A,求实数a的取值范围.
考点:交集及其运算,并集及其运算
专题:集合
分析:(Ⅰ)将a=3代入A与B中确定出A与B,求出A∪B即可;
(Ⅱ)由A∩B=A,得到A为B的子集,分a=-1,a<-1和a>-1三种情况,分别确定出a的范围即可.
(Ⅱ)由A∩B=A,得到A为B的子集,分a=-1,a<-1和a>-1三种情况,分别确定出a的范围即可.
解答:
解:(Ⅰ)将a=3代入A中不等式得:x2-2x-15<0,即(x-5)(x+3)<0,
解得:-3<x<5,即A=(-3,5);
将a=3代入B中等式得:y=3x-6,
∵x≤2,
∴0<3x≤9,即-6<y=3x-6≤3,
∴B=(-6,3],
则A∪B=(-6,5);
(Ⅱ)∵A∩B=A,
∴A⊆B,
由B中y的范围为-2a<y≤9-2a,即B=(-2a,9-2a),
由A中不等式变形得:x2-2x+1-a2-2a-1<0,
即(x-1)2-(a+1)2<0,
整理得:(x+a)(x-a-2)<0,
∵A∩B=A,∴A⊆B,
当a=-1时,A=∅,满足题意;
当a+2>-a,即a>-1时,A=(-a,a+2),
∵A⊆B,
∴
,
解得:0≤a≤
;
当a+2<-a,即a<-1时,A=(a+2,-a),
∵A⊆B,∴
,
解得:-
≤a≤9(舍去),
综上,a=-1或0≤a≤
.
解得:-3<x<5,即A=(-3,5);
将a=3代入B中等式得:y=3x-6,
∵x≤2,
∴0<3x≤9,即-6<y=3x-6≤3,
∴B=(-6,3],
则A∪B=(-6,5);
(Ⅱ)∵A∩B=A,
∴A⊆B,
由B中y的范围为-2a<y≤9-2a,即B=(-2a,9-2a),
由A中不等式变形得:x2-2x+1-a2-2a-1<0,
即(x-1)2-(a+1)2<0,
整理得:(x+a)(x-a-2)<0,
∵A∩B=A,∴A⊆B,
当a=-1时,A=∅,满足题意;
当a+2>-a,即a>-1时,A=(-a,a+2),
∵A⊆B,
∴
|
解得:0≤a≤
| 7 |
| 3 |
当a+2<-a,即a<-1时,A=(a+2,-a),
∵A⊆B,∴
|
解得:-
| 2 |
| 3 |
综上,a=-1或0≤a≤
| 7 |
| 3 |
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算:sin225°的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
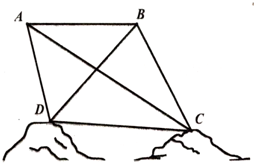 为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为
为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为