题目内容
解关于x的不等式x2-ax+2≤0(a∈R).
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:先计算出该不等式对应方程得判别式,然后通过讨论判别式的符号来判断该不等式对应函数与x轴的位置关系,然后根据图象写出不等式的解.
解答:
解:∵△=a2-8,
①当△>0,即a>2
或a<-2
时,
由x2-ax+2=0得x1,2=
或
,
此时原不等式的解为
≤x≤
;
②当△=0,即a=-2
或2
时,
若a=2
,则不等式的解为x=
,
若a=-2
,则不等式的解为x=-
;
③当△<0,即-2
<a<2
时,
原不等式无解.
综上,当a>2
或a<-2
时,原不等式的解为
≤x≤
;
当a=2
时,则不等式的解为x=
,
当a=-2
,则不等式的解为x=-
;
当-2
<a<2
时,原不等式无解.
①当△>0,即a>2
| 2 |
| 2 |
由x2-ax+2=0得x1,2=
a-
| ||
| 2 |
a+
| ||
| 2 |
此时原不等式的解为
a-
| ||
| 2 |
a+
| ||
| 2 |
②当△=0,即a=-2
| 2 |
| 2 |
若a=2
| 2 |
| 2 |
若a=-2
| 2 |
| 2 |
③当△<0,即-2
| 2 |
| 2 |
原不等式无解.
综上,当a>2
| 2 |
| 2 |
a-
| ||
| 2 |
a+
| ||
| 2 |
当a=2
| 2 |
| 2 |
当a=-2
| 2 |
| 2 |
当-2
| 2 |
| 2 |
点评:解一元二次不等式的基本思想是函数思想、数形结合及分类讨论思想,讨论的依据一般是函数图象与x轴的位置关系,然后根据图象写出不等式的解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
根据图所示的算法流程图,输出的结果T为( )


| A、8 | B、48 | C、49 | D、50 |
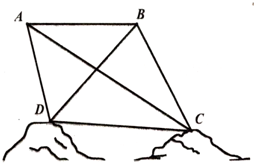 为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为
为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为