题目内容
已知x∈R，求证：x6-x5+x2-x+1＞0．
考点：函数恒成立问题
专题：证明题,不等式的解法及应用
分析：分类讨论，即可证明结论．
解答：
证明：①x≥1时，x6＞x5，x2≥x，1＞0．相加得，x6+x2+1＞x5+x，∴x6-x5+x2-x+1＞0；
②0＜x＜1时，x2＞x5，1＞x，x6＞0，∴x6-x5+x2-x+1＞0；
③x＜0时，-x5＞0，-x＞0，x6+x2+1＞0，∴x6-x5+x2-x+1＞0；
④x=0时，左式=1＞0．
综上知，对任意实数x6-x5+x2-x+1＞0恒成立．
②0＜x＜1时，x2＞x5，1＞x，x6＞0，∴x6-x5+x2-x+1＞0；
③x＜0时，-x5＞0，-x＞0，x6+x2+1＞0，∴x6-x5+x2-x+1＞0；
④x=0时，左式=1＞0．
综上知，对任意实数x6-x5+x2-x+1＞0恒成立．
点评：本题考查不等式的证明，考查分类讨论的数学思想，比较基础．
练习册系列答案
相关题目
一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{an}，若a8=15，且a1，a2，a5成等比数列，则此样本的平均数和中位数分别是（ ）
| A、11，10 |
| B、10，10 |
| C、11，12 |
| D、10，12 |
计算：sin225°的值为（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
如图，△ABC的两边AB=2，AC=1，点D在BC边上，且满足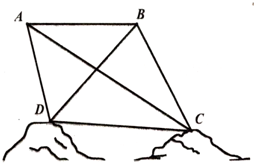
为了绘制海底地图，测量海底两点C，D间的距离，海底探测仪沿水平方向在A，B两点进行测量，A，B，C，D在同一个铅垂平面内．海底探测仪测得∠BAC=30°，∠DAC=45°，∠ABD=45°，∠DBC=75°，A，B两点的距离为