题目内容
过曲线y=
x3上的点(1,
)作曲线的切线m,则该切线m与圆O:x2+y2=1相交的弦长为 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:先求出切线m的方程,再利用勾股定理,计算切线m与圆O:x2+y2=1相交的弦长.
解答:
解:由题意,点(1,
)为切点,则
∵y=
x3,
∴y′=
x2,
∴x=1时,y′=
,y=
,
∴切线m:y-
=
(x-1),即3x-2y-2=0,
∴圆心到直线的距离为
,
∴切线m与圆O:x2+y2=1相交的弦长为2
=
.
故答案为:
.
| 1 |
| 2 |
∵y=
| 1 |
| 2 |
∴y′=
| 3 |
| 2 |
∴x=1时,y′=
| 3 |
| 2 |
| 1 |
| 2 |
∴切线m:y-
| 1 |
| 2 |
| 3 |
| 2 |
∴圆心到直线的距离为
| 2 | ||
|
∴切线m与圆O:x2+y2=1相交的弦长为2
1-
|
6
| ||
| 13 |
故答案为:
6
| ||
| 13 |
点评:本小题主要考查导数的几何意义、利用导数研究曲线上某点切线方程、直线与圆的位置关系等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
已知sinα-sinβ=
,cosα-cosβ=
,则cos2
等于( )
| ||
| 3 |
| ||
| 3 |
| α-β |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
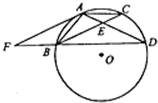 如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=